5.已知双曲线${C_1}:\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0,b>0)$,抛物线${C_2}:{y^2}=4x$,C1与C2有公共的焦点F,C1与C2在第一象限的公共点为M,直线MF的倾斜角为θ,且$cosθ=\frac{1-2a}{3-2a}$,则关于双曲线的离心率的说法正确的是( )
| A. | 仅有两个不同的离心率e1,e2且e1∈(1,2),e2∈(4,6) | |
| B. | 仅有两个不同的离心率e1,e2且e1∈(2,3),e2∈(4,6) | |
| C. | 仅有一个离心率e且e∈(2,3) | |
| D. | 仅有一个离心率e且e∈(3,4) |
4.在△ABC中$A=\frac{π}{3},b+c=4,E、F$为边BC的三等分点,则$\overrightarrow{AE}$•$\overrightarrow{AF}$的最小值为( )
| A. | $\frac{{9\sqrt{3}}}{2}$ | B. | $\frac{8}{3}$ | C. | $\frac{26}{9}$ | D. | 3 |
3.设函数f(x)的定义域为D,若f(x)满足条件:存在[a,b]⊆D(a<b),使f(x)在[a,b]上的值域也是[a,b],则称为“优美函数”,若函数$f(x)={log_2}({4^x}+t)$为“优美函数”,则t的取值范围是( )
| A. | $(\frac{1}{4},+∞)$ | B. | (0,1) | C. | $(0,\frac{1}{2})$ | D. | $(0,\frac{1}{4})$ |
2.(1-2x)5的展开式中含x3的系数为( )
| A. | -80 | B. | 80 | C. | 10 | D. | -10 |
1.若z=1-i,则复数z+z2在复平面上对应的点的坐标为( )
| A. | (1,-3) | B. | (-3,1) | C. | (1,1) | D. | (-1,1) |
18.已知F1,F2为双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a,b>0)$的左右焦点,过F1的直线l与圆x2+y2=b2相切于点M,且|MF2|=2|MF1|,则直线l的斜率是( )
| A. | $\frac{{\sqrt{3}}}{2}$ | B. | $\frac{{\sqrt{7}}}{2}$ | C. | $±\frac{{\sqrt{3}}}{2}$ | D. | $±\frac{{\sqrt{7}}}{2}$ |
17.已知等差数列{an}中,a2=4,a5=7,m,n∈N+,满足a1m+a2m+a3m+…+anm=an+1m,则n等于( )
| A. | 1和2 | B. | 2和3 | C. | 3和4 | D. | 2和4 |
16. 如图是一个正三棱柱挖去一个圆柱得到的一个几何体的三视图,则该几何体的体积与挖去的圆柱的体积比为( )
如图是一个正三棱柱挖去一个圆柱得到的一个几何体的三视图,则该几何体的体积与挖去的圆柱的体积比为( )
0 240309 240317 240323 240327 240333 240335 240339 240345 240347 240353 240359 240363 240365 240369 240375 240377 240383 240387 240389 240393 240395 240399 240401 240403 240404 240405 240407 240408 240409 240411 240413 240417 240419 240423 240425 240429 240435 240437 240443 240447 240449 240453 240459 240465 240467 240473 240477 240479 240485 240489 240495 240503 266669
 如图是一个正三棱柱挖去一个圆柱得到的一个几何体的三视图,则该几何体的体积与挖去的圆柱的体积比为( )
如图是一个正三棱柱挖去一个圆柱得到的一个几何体的三视图,则该几何体的体积与挖去的圆柱的体积比为( )| A. | $\frac{{3\sqrt{3}}}{π}-1$ | B. | $\frac{{3\sqrt{3}}}{π}-\frac{1}{3}$ | C. | $\frac{{3\sqrt{3}}}{π}$ | D. | $\frac{{3\sqrt{3}}}{π}+1$ |
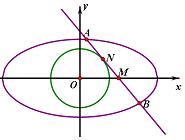 已知椭圆$C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的右焦点$(\sqrt{3},0)$,且经过点$(-1,\frac{{\sqrt{3}}}{2})$,点M是x轴上的一点,过点M的直线l与椭圆C交于A,B两点(点A在x轴的上方)
已知椭圆$C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的右焦点$(\sqrt{3},0)$,且经过点$(-1,\frac{{\sqrt{3}}}{2})$,点M是x轴上的一点,过点M的直线l与椭圆C交于A,B两点(点A在x轴的上方)