5．函数$f{x^{{m^2}+m-3}}$是定义域为R的幂函数.且当x∈是增函数.得解析式．≤8.则a的取值范围．——青夏教育精英家教网——

5．函数$f（x）=（{{m^2}-m-1}）{x^{{m^2}+m-3}}$是定义域为R的幂函数，且当x∈（0，+∞）时，f（x）是增函数，
（1）求m的值，并写出f（x）得解析式．
（2）若f（a）≤8，则a的取值范围．

4．已知函数f（x）=ax²+bx+3a+b为偶函数，其定义域为[a-3，2a]，则a+b的值为（　　）

3．函数$f（x）=sin（x+\frac{π}{6}）cos（x+\frac{π}{6}）$，给出下列结论正确的是（　　）

	A．	f（x）的最小正周期为 $\frac{π}{2}$		B．	f（x）的一条对称轴为$x=\frac{π}{6}$
	C．	f（x）的一个对称中心为$（\frac{π}{6}，0）$		D．	$f（x-\frac{π}{6}）$是奇函数

2．已知f（x）=ax³+bx+4其中a，b为常数，若f（-2）=-2，则f（2）的值等于（　　）

1．已知f（x）=$\left\{\begin{array}{l}{{x}^{2}，x＞0}\\{π，x=0}\\{0，x＜0}\end{array}\right.$，则f（-π）等于（　　）

20．计算[（-2）^-2]${\;}^{\frac{1}{2}}$的结果是（　　）

19．若直线l₁：3x+y-3=0与l₂：3x+my+1=0平行，则它们之间的距离为$\frac{2\sqrt{10}}{5}$．

18．已知函数f（x）=cosx，a，b，c分别为△ABC的内角A，B，C所对的边，且3a²+3b²-c²=4ab，则下列不等式一定成立的是（　　）

f（sinA）≤f（cosB）

f（sinA）≤f（sinB）

f（cosA）≤f（sinB）

f（cosA）≤f（cosB）

17．已知函数$f（x）=\frac{1}{3}{x^3}-e{x^2}+mx+1$，$g（x）=\frac{lnx}{x}$．
（Ⅰ）函数f（x）在点（1，f（1））处的切线与直线（1-2e）x-y+4=0平行，求函数f（x）的单调区间；
（Ⅱ）设函数f（x）的导函数为f′（x），对任意的x₁，x₂∈（0，+∞），若g（x₁）＜f′（x₂）恒成立，求m的取值范围．

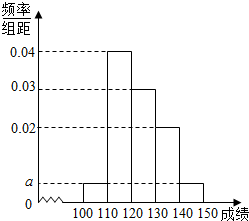贵阳市某中学高三第一次摸底考试中100名学生数学成绩的频率分布直方图如图所示，其中成绩分组区间是[100，110），[110，120），[120，130），[130，140），[140，150]．
（Ⅰ）求图中a的值；
（Ⅱ）根据频率分布直方图，估计这100名学生数学成绩的平均分；
（Ⅲ）若这100名学生数学成绩某些分数段的人数（x）与语文成绩相应分数段的人数（y）之比如下表所示，求语文成绩在[100，140）之外的人数．

分数段	[100，110）	[110，120）	[120，130）	[130，140）
x：y	1：1	2：1	3：4	4：5

0 224110 224118 224124 224128 224134 224136 224140 224146 224148 224154 224160 224164 224166 224170 224176 224178 224184 224188 224190 224194 224196 224200 224202 224204 224205 224206 224208 224209 224210 224212 224214 224218 224220 224224 224226 224230 224236 224238 224244 224248 224250 224254 224260 224266 224268 224274 224278 224280 224286 224290 224296 224304 266669