我们把使得f(x)=0的实数x叫做函数y=f(x)的零点,对于区间[a,b]上的连续函数y=f(x),若f(a)•f(b)<0,那么函数y=f(x)在区间(a,b)内有零点,则函数f(x)=lgx-
的零点所在的区间应是( )
| 2 |
| x |
| A、(1,2) |
| B、(2,3) |
| C、(3,4) |
| D、(4,5) |
如下图①对应于函数f(x),则在下列给出的四个函数中,图②对应的函数只能是( )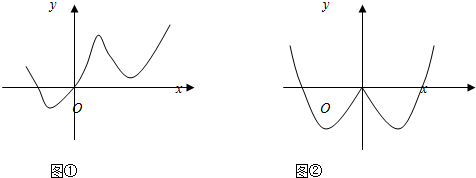

| A、y=f(|x|) |
| B、y=|f(x)| |
| C、y=f(-|x|) |
| D、y=-f(|x|) |
已知△ABC中,
+
=
,则D点位于( )
| ||
|
|
| ||
|
|
| AD |
| A、BC边的中线上 |
| B、BC边的高线上 |
| C、BC边的中垂线上 |
| D、∠BAC的平分线上 |
已知函数f(x)=x+
-2在区间(2,4)内有唯一零点,则b的取值范围是( )
| b |
| x |
| A、R |
| B、(-∞,0) |
| C、(-8,+∞) |
| D、(-8,0) |