题目内容
已知函数f(x)满足(
)f(x)=x+1,f-1(x)是f(x)的反函数,则函数y=f-1(x-1)的图象是( )
| 1 |
| 2 |
A、 |
B、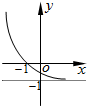 |
C、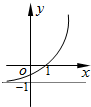 |
D、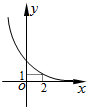 |
考点:反函数,指数函数的图像与性质
专题:函数的性质及应用
分析:(
)f(x)=x+1,解得x=(
)y-1,可得f-1(x)=(
)x-1,函数y=f-1(x-1)=(
)x-1-1,由于其图象单调递减,且经过(1,0),即可得出.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解答:
解:∵(
)f(x)=x+1,解得x=(
)y-1,
把x与y互换可得:y=(
)x-1,
∴f-1(x)=(
)x-1,
∴函数y=f-1(x-1)=(
)x-1-1,
其图象单调递减,且经过(1,0),
故选:A.
| 1 |
| 2 |
| 1 |
| 2 |
把x与y互换可得:y=(
| 1 |
| 2 |
∴f-1(x)=(
| 1 |
| 2 |
∴函数y=f-1(x-1)=(
| 1 |
| 2 |
其图象单调递减,且经过(1,0),
故选:A.
点评:本题考查了反函数的求法、函数的性质,考查了数形结合的思想方法,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
一个命题与他们的逆命题、否命题、逆否命题这4个命题中( )
| A、真命题与假命题的个数相同 |
| B、真命题的个数一定是奇数 |
| C、真命题的个数一定是偶数 |
| D、真命题的个数可能是奇数,也可能是偶数 |
如下图①对应于函数f(x),则在下列给出的四个函数中,图②对应的函数只能是( )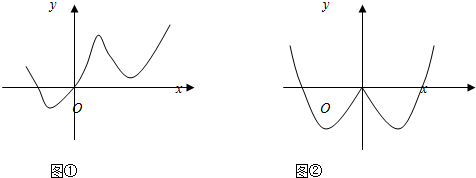

| A、y=f(|x|) |
| B、y=|f(x)| |
| C、y=f(-|x|) |
| D、y=-f(|x|) |
已知sina=
,且a是第二象限角,则tana[cos(π-a)+sin(π+a)]的值等于( )
| 3 |
| 5 |
A、
| ||
B、
| ||
C、-
| ||
D、-
|
设f (x)=
,则f(f(x))(x∈R) 的值为( )
|
| A、0 | B、1 |
| C、0或1 | D、以上都不对 |