用数学归纳法证明不等式“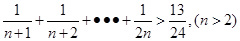 ”的过程中,由n=k到n=k+1时,不等式的左边( )
”的过程中,由n=k到n=k+1时,不等式的左边( )
A.增加了一项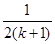 |
B.增加了两项 |
C.增加了一项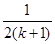 ,又减少了一项 ,又减少了一项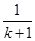 |
D.增加了两项 ,又减少了一项 ,又减少了一项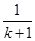 |
用反证法证明命题“若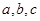 都是正数,则
都是正数,则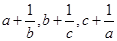 三数中至少有一个不小于
三数中至少有一个不小于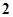 ”,提出的假设是( )
”,提出的假设是( )
A.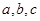 不全是正数 不全是正数 |
B.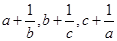 至少有一个小于 至少有一个小于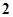 |
C.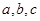 都是负数 都是负数 |
D.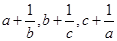 都小于2 都小于2 |
把1,3,6,10,15,21,…这些数叫做三角形数,这是因为这些数目的点子可以排成一个正三角形,则第七个三角形数是( )
| A.21 | B.28 | C.32 | D.36 |
用反证法证明“如果a>b,那么 >
> ”假设的内容应是( )
”假设的内容应是( )
A. = = | B. < < |
C. = = 且 且 < < | D. = = 或 或 < < |
下列说法正确的个数是 ( )
①演绎推理是由一般到特殊的推理
②演绎推理得到的结论一定是正确的
③演绎推理的一般模式是“三段论”形式
④演绎推理得到的结论的正误与大前提、小前提和推理形式有关
| A.1 | B.2 | C.3 | D.4 |
用数学归纳法证明: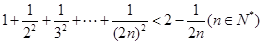 ,第二步证明“从
,第二步证明“从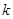 到
到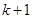 ”,左端增加的项数是( )
”,左端增加的项数是( )
A.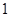 | B.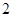 | C.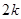 | D.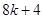 |
在平面上,若两个正三角形的边长比为1:2.则它们的面积之比为1:4.类似地,在空间中,若两个正四面体的棱长比为1:2,则它们的体积比为( )
| A.1:2 | B.1:4 | C.1:6 | D.1:8 |
在用数学归纳法证明 时,在验证当
时,在验证当 时,等式左边为( )
时,等式左边为( )
| A.1 | B. | C. | D. |
由“半径为R的圆内接矩形中,正方形的面积最大”,推理出“半径为R的球的内接长方体中,正方体的体积最大”是( )
| A.归纳推理 | B.类比推理 | C.演绎推理 | D.以上都不是 |
有一段演绎推理是这样的,“有些有理数是分数,整数是有理数,则整数是分数”,结论显然是错误的,因为
| A.大前提错误 | B.小前提错误 | C.推理形式错误 | D.非以上错误 |