题目内容
用反证法证明命题“若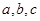 都是正数,则
都是正数,则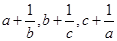 三数中至少有一个不小于
三数中至少有一个不小于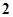 ”,提出的假设是( )
”,提出的假设是( )
A.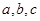 不全是正数 不全是正数 |
B.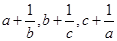 至少有一个小于 至少有一个小于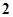 |
C.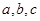 都是负数 都是负数 |
D.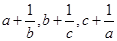 都小于2 都小于2 |
D
解析试题分析:根据反证法的思路可知,将结论变为否定来加以证明,即“若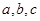 都是正数,则
都是正数,则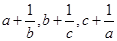 三数中至少有一个不小于
三数中至少有一个不小于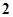 ”,提出的假设为
”,提出的假设为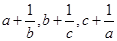 都小于2,选D.
都小于2,选D.
考点:反证法
点评:本题主要考查求一个命题的否定,用反证法证明数学命题,把要证的结论进行否定,得到要证的结论的反面,是解题的突破口,属于基础题.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
用反证法证明命题:“一个三角形中不能有两个直角”的过程归纳为以下三个步骤:
① ,这与三角形内角和为
,这与三角形内角和为 相矛盾,
相矛盾, 不成立;②所以一个三角形中不能有两个直角;③假设三角形的三个内角
不成立;②所以一个三角形中不能有两个直角;③假设三角形的三个内角 、
、 、
、 中有两个直角,不妨设
中有两个直角,不妨设 ,正确顺序的序号为
,正确顺序的序号为
| A.①②③ | B.③①② | C.①③② | D.②③① |
下列三句话按三段论的模式排列顺序正确的是( )
① 2013不能被2整除; ② 一切奇数都不能被2整除; ③ 2013是奇数;
| A.①②③ | B.②①③ | C.②③① | D.③②① |
在平面上,若两个正三角形的边长比为1:2.则它们的面积之比为1:4.类似地,在空间中,若两个正四面体的棱长比为1:2,则它们的体积比为( )
| A.1:2 | B.1:4 | C.1:6 | D.1:8 |
根据偶函数定义可推得“函数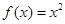 在
在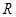 上是偶函数”的推理过程是( )
上是偶函数”的推理过程是( )
| A.归纳推理 | B.类比推理 | C.演绎推理 | D.非以上答案 |
在用数学归纳法证明凸n边形内角和定理时,第一步应验证( )
| A.n=1时成立 | B.n=2时成立 |
| C.n=3时成立 | D.n=4时成立 |
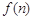 表示第
表示第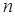 幅图的蜂巢总数,则
幅图的蜂巢总数,则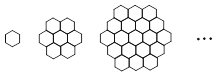
 .
.