题目内容
由“半径为R的圆内接矩形中,正方形的面积最大”,推理出“半径为R的球的内接长方体中,正方体的体积最大”是( )
| A.归纳推理 | B.类比推理 | C.演绎推理 | D.以上都不是 |
B
解析试题分析:类比推理的一般步骤是:(1)找出两类事物之间的相似性或一致性;(2)用一类事物的性质去推测另一类事物的性质,得出一个明确的命题(猜想).所以,由“半径为R的圆内接矩形中,正方形的面积最大”,推理出“半径为R的球的内接长方体中,正方体的体积最大”是类比推理。选B。
考点:本题主要考查类比推理。
点评:简单题,类比推理的一般步骤是:(1)找出两类事物之间的相似性或一致性;(2)用一类事物的性质去推测另一类事物的性质,得出一个明确的命题(猜想).

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
下列平面图形中与空间的平行六面体作为类比对象较合适的是( )
| A.三角形 | B.梯形 | C.平行四边形 | D.矩形 |
下列三句话按三段论的模式排列顺序正确的是( )
① 2013不能被2整除; ② 一切奇数都不能被2整除; ③ 2013是奇数;
| A.①②③ | B.②①③ | C.②③① | D.③②① |
用反证法证明“如果a>b,那么 >
> ”假设的内容应是( )
”假设的内容应是( )
A. = = | B. < < |
C. = = 且 且 < < | D. = = 或 或 < < |
根据偶函数定义可推得“函数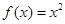 在
在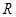 上是偶函数”的推理过程是( )
上是偶函数”的推理过程是( )
| A.归纳推理 | B.类比推理 | C.演绎推理 | D.非以上答案 |
定义平面向量之间的一种运算“☉”如下:对任意的a=(m,n),b=(p,q),令a☉b=mq-np.下面说法错误的是( )
| A.若a与b共线,则a☉b=0 |
| B.a☉b=b☉a |
| C.对任意的λ∈R,有(λa)☉b=λ(a☉b) |
| D.(a☉b)2+(a·b)2=|a|2|b|2 |
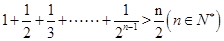 ,第二步由k到k+1时不等式左边需增加( )
,第二步由k到k+1时不等式左边需增加( )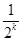
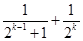
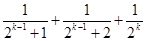
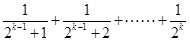
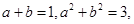
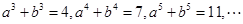 ,则依次类推可得
,则依次类推可得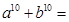 ;
; ,所以36的所有正约数之和为
,所以36的所有正约数之和为