观察下列各式:72=49,73=343,74=2401,…,则72011的末两位数字为( )
| A.01 | B.43 |
| C.07 | D.49 |
观察下列事实:|x|+|y|=1的不同整数解(x,y)的个数为4,|x|+|y|=2的不同整数解(x,y)的个数为8,|x|+|y|=3的不同整数解(x,y)的个数为12,…,则|x|+|y|=20的不同整数解(x,y)的个数为( )
| A.76 | B.80 |
| C.86 | D.92 |
右图1是一个水平摆放的小正方体木块,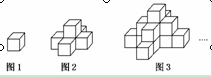
图2、图3是由这样的小正方体木块叠放而成,按照这样的规律继续逐个叠放下去,那么在第七个叠放的图形中小正方体木块数应是( )
| A.25 | B.66 | C.91 | D.120 |
把数列 的各项按顺序排列成如下的三角形状,
的各项按顺序排列成如下的三角形状,
记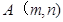 表示第
表示第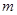 行的第
行的第 个数,若
个数,若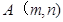 =
=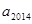 ,则
,则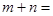 ( )
( )
| A.122 | B.123 | C.124 | D.125 |
某个命题与正整数有关,如果当n=k(k∈N+)时,该命题成立,那么可
推得当n=k+1时命题也成立.现在已知当n=5时,该命题不成立,那么可推得( ).
| A.当n=6时该命题不成立 |
| B.当n=6时该命题成立 |
| C.当n=4时该命题不成立 |
| D.当n=4时该命题成立 |
下列推理是归纳推理的是( ).
| A.A,B为定点,动点P满足|PA|+|PB|=2a>|AB|,得P的轨迹为椭圆 |
| B.由a1=1,an=3n-1,求出S1,S2,S3,猜想出数列的前n项和Sn的表达式 |
C.由圆x2+y2=r2的面积πr2,猜出椭圆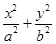 =1的面积S=πab =1的面积S=πab |
| D.科学家利用鱼的沉浮原理制造潜艇 |
设S(n)= ,则( ).
,则( ).
A.S(n)共有n项,当n=2时,S(2)= |
B.S(n)共有n+1项,当n=2时,S(2)= |
C.S(n)共有n2-n项,当n=2时,S(2)= |
D.S(n)共有n2-n+1项,当n=2时,S(2)= |
学习合情推理后,甲、乙两位同学各举了一个例子,
甲:由“若三角形周长为l,面积为S,则其内切圆半径r=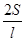 ”类比可得“若三棱锥表面积为S,体积为V,则其内切球半径r=
”类比可得“若三棱锥表面积为S,体积为V,则其内切球半径r=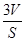 ”;
”;
乙:由“若直角三角形两直角边长分别为a、b,则其外接圆半径r=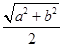 ”类比可得“若三棱锥三条侧棱两两垂直,侧棱长分别为a、b、c,则其外接球半径r=
”类比可得“若三棱锥三条侧棱两两垂直,侧棱长分别为a、b、c,则其外接球半径r=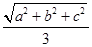 ”.这两位同学类比得出的结论( )
”.这两位同学类比得出的结论( )
| A.两人都对 | B.甲错、乙对 |
| C.甲对、乙错 | D.两人都错 |
用数学归纳法证明“n3+(n+1)3+(n+2)3,(n∈N+)能被9整除”,要利
用归纳法假设证n=k+1时的情况,只需展开( ).
| A.(k+3)3 | B.(k+2)3 |
| C.(k+1)3 | D.(k+1)3+(k+2)3 |
在数列{an}中,an=1-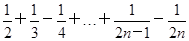 则ak+1=( ).
则ak+1=( ).
A.ak+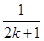 | B.ak+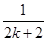 - -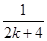 |
C.ak+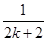 | D.ak+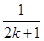 - -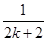 |