题目内容
某个命题与正整数有关,如果当n=k(k∈N+)时,该命题成立,那么可
推得当n=k+1时命题也成立.现在已知当n=5时,该命题不成立,那么可推得( ).
| A.当n=6时该命题不成立 |
| B.当n=6时该命题成立 |
| C.当n=4时该命题不成立 |
| D.当n=4时该命题成立 |
C
解析

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知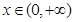 有下列各式:
有下列各式: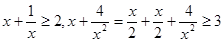 ,
,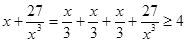 成立,观察上面各式,按此规律若
成立,观察上面各式,按此规律若 ,则正数
,则正数 ( )
( )
| A.4 | B.5 | C.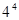 | D.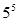 |
用数学归纳法证明1+2+3+…+(2n+1)=(n+1)(2n+1)时,从n=k到n=k+1,左边需增添的代数式是( )
| A.2k+2 | B.2k+3 |
| C.2k+1 | D.(2k+2)+(2k+3) |
用反证法证明“a,b,c中至少有一个大于0”,下列假设正确的是( )
| A.假设a,b,c都小于0 |
| B.假设a,b,c都大于0 |
| C.假设a,b,c中都不大于0 |
| D.假设a,b,c中至多有一个大于0 |
在数列{an}中,an=1-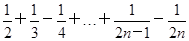 则ak+1=( ).
则ak+1=( ).
A.ak+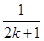 | B.ak+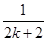 - -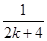 |
C.ak+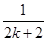 | D.ak+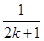 - -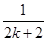 |
在集合{a,b,c,d}上定义两种运算⊕和?如下:
那么d?(a⊕c)等于( )
| A.a | B.b | C.c | D.d |
下列表述正确的是 ( )
①归纳推理是由部分到整体的推理;②归纳推理是由一般到一般的推理;③演绎推理是由一般到特殊的推理;④类比推理是由特殊到一般的推理;⑤类比推理是由特殊到特殊的推理.
| A.①②③ | B.②③④ |
| C.②④⑤ | D.①③⑤ |
推理“①矩形是平行四边形;②正方形是矩形;③正方形是平行四边形”中的小前提是( )
| A.① | B.② |
| C.③ | D.以上均错 |
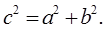 设想正方形换成正方体,把截线换成如图的截面,这时从正方体上截下三条侧棱两两垂直的三棱锥O—LMN,如果用
设想正方形换成正方体,把截线换成如图的截面,这时从正方体上截下三条侧棱两两垂直的三棱锥O—LMN,如果用 表示三个侧面面积,
表示三个侧面面积, 表示截面面积,那么你类比得到的结论是( )
表示截面面积,那么你类比得到的结论是( )