题目内容
设S(n)= ,则( ).
,则( ).
A.S(n)共有n项,当n=2时,S(2)= |
B.S(n)共有n+1项,当n=2时,S(2)= |
C.S(n)共有n2-n项,当n=2时,S(2)= |
D.S(n)共有n2-n+1项,当n=2时,S(2)= |
D
解析

练习册系列答案
相关题目
用演绎法证明函数 是增函数时的小前提是( )
是增函数时的小前提是( )
| A.增函数的定义 | B.函数 满足增函数的定义 满足增函数的定义 |
C.若 ,则 ,则 | D.若 ,则 ,则 |
用反证法证明命题“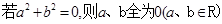 ”,其反设正确的是( )
”,其反设正确的是( )
A.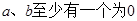 | B.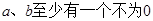 |
C.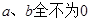 | D. |
不相等的三个正数a、b、c成等差数列,并且x是a、b的等比中项,y是b、c的等比中项,则x2、b2、y2三数( )
| A.成等比数列而非等差数列 |
| B.成等差数列而非等比数列 |
| C.既成等差数列又成等比数列 |
| D.既非等差数列又非等比数列 |
“因为指数函数y=ax是增函数,而 是指数函数,所以
是指数函数,所以 是增函数.”在以上三段论推理中( )
是增函数.”在以上三段论推理中( )
| A.大前提错误 |
| B.小前提错误 |
| C.推理形式错误 |
| D.大前提、小前提、推理形式错均正确 |
设n是自然数,则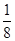 (n2-1)[1-(-1)n]的值 ( )
(n2-1)[1-(-1)n]的值 ( )
| A.一定是零 | B.不一定是整数 |
| C.一定是偶数 | D.是整数但不一定是偶数 |
观察下列事实:|x|+|y|=1的不同整数解(x,y)的个数为4,|x|+|y|=2的不同整数解(x,y)的个数为8,|x|+|y|=3的不同整数解(x,y)的个数为12,…,则|x|+|y|=20的不同整数解(x,y)的个数为( )
| A.76 | B.80 |
| C.86 | D.92 |
观察下列各式:55=3 125,56=15 625,57=78 125,…,则52 011
的末四位数字为 ( ).
| A.3 125 | B.5 625 |
| C.0 625 | D.8 125 |
下列推理中属于归纳推理且结论正确的是( )
| A.设数列{an}的前n项和为Sn.由an=2n-1,求出S1=12,S2=22,S3=32,…,推断:Sn=n2 |
| B.由f(x)=xcos x满足f(-x)=-f(x)对?x∈R都成立,推断:f(x)=xcos x为奇函数 |
C.由圆x2+y2=r2的面积S=πr2,推断:椭圆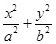 =1(a>b>0)的面积S=πab =1(a>b>0)的面积S=πab |
| D.由(1+1)2>21,(2+1)2>22,(3+1)2>23,…,推断:对一切n∈N*,(n+1)2>2n |