表示不超过
的最大整数，例如：
．
依此规律，那么
（ ）
A． | B． | C． | D． |
演绎推理“因为对数函数
是增函数，而函数
是对数函数，所以是增函数”所得结论错误的原因是（ ）
| A．大前提错误 | B．小前提错误 |
| C．推理形式错误 | D．大前提和小前提都错误 |
用数学归纳法证明“n3＋(n＋1)3＋(n＋2)3(n∈N*)能被9整除”，要利用归纳假设证n＝k＋1时的情况，只需展开( )
| A．(k＋3)3 | B．(k＋2)3 |
| C．(k＋1)3 | D．(k＋1)3＋(k＋2)3 |
平面内有n条直线，最多可将平面分成f(n)个区域，则f(n)的表达式为( )
| A．n＋1 | B．2n |
C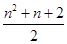． | D．n2＋n＋1 |
用数学归纳法证明1＋2＋3＋…＋(2n＋1)＝(n＋1)(2n＋1)时，从n＝k到n＝k＋1，左边需增添的代数式是( )
| A．2k＋2 | B．2k＋3 |
| C．2k＋1 | D．(2k＋2)＋(2k＋3) |
若a，b∈R，则下面四个式子中恒成立的是( )
| A．lg(1＋a2)>0 | B．a2＋b2≥2(a－b－1) |
| C．a2＋3ab>2b2 | D． < |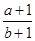
不相等的三个正数a、b、c成等差数列，并且x是a、b的等比中项，y是b、c的等比中项，则x2、b2、y2三数( )
| A．成等比数列而非等差数列 |
| B．成等差数列而非等比数列 |
| C．既成等差数列又成等比数列 |
| D．既非等差数列又非等比数列 |
用反证法证明某命题时，对结论：“自然数a，b，c中恰有一个偶数”正确的反设为( )
| A．a，b，c中至少有两个偶数 |
| B．a，b，c中至少有两个偶数或都是奇数 |
| C．a，b，c都是奇数 |
| D．a，b，c都是偶数 |
设a，b是两个实数，给出下列条件：
①a＋b>1；②a＋b＝2；③a＋b>2；④a2＋b2>2；⑤ab>1.
其中能推出：“a，b中至少有一个大于1”的条件是( )
| A．②③ | B．①②③ | C．③ | D．③④⑤ |
分析法又称执果索因法，若用分析法证明：“设a>b>c，且a＋b＋c＝0，求证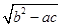 
<
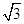a”索的因应是( )
| A．a－b>0 | B．a－c>0 |
| C．(a－b)(a－c)>0 | D．(a－b)(a－c)<0 |