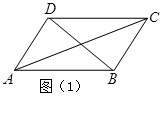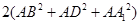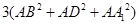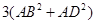用火柴棒摆“金鱼”,如图所示: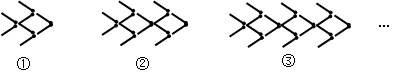
按照上面的规律,第4个“金鱼”图需要火柴棒的根数为
| A.24 | B.26 | C.28 | D.30 |
根据偶函数定义可推得“函数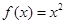 在
在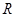 上是偶函数”的推理过程是( )
上是偶函数”的推理过程是( )
| A.归纳推理 | B.类比推理 | C.演绎推理 | D.非以上答案 |
用反证法证明命题“三角形的内角至多有一个钝角”时,假设的内容应为( )
| A.假设至少有一个钝角 | B.假设至少有两个钝角 |
| C.假设没有一个钝角 | D.假设没有一个钝角或至少有两个钝角 |
推理:因为平行四边形对边平行且相等,而矩形是特殊的平行四边形,所以矩形的对边平行且相等.以上推理的方法是( )
| A.合情推理 | B.演绎推理 | C.归纳推理 | D.类比推理 |
法国数学家费马观察到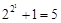 ,
, ,
, ,
, 都是质数,于是他提出猜想:任何形如
都是质数,于是他提出猜想:任何形如 N*)的数都是质数,这就是著名的费马猜想. 半个世纪之后,善于发现的欧拉发现第5个费马数
N*)的数都是质数,这就是著名的费马猜想. 半个世纪之后,善于发现的欧拉发现第5个费马数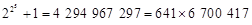 不是质数,从而推翻了费马猜想,这一案例说明( )
不是质数,从而推翻了费马猜想,这一案例说明( )
| A.归纳推理,结果一定不正确 | B.归纳推理,结果不一定正确 |
| C.类比推理,结果一定不正确 | D.类比推理,结果不一定正确 |
用反证法证明命题“三角形的内角至少有一个不大于60°”时,应该先
| A.假设三内角都不大于60° |
| B.假设三内角都大于60° |
| C.假设三内角至多有一个大于60° |
| D.假设三内角至多有两个大于60° |
根据给出的数塔猜测123 456×9+7= ( )
1×9+2=11
12×9+3=111
123×9+4=1 111
1 234×9+5=11 111
12 345×9+6=111 111
……
| A.1 111 110 | B.1 111 111 |
| C.1 111 112 | D.1 111 113 |
用反证法证明命题“三角形的内角中至多有一个钝角”时,假设正确的是( )
| A.三个内角中至少有一个钝角 |
| B.三个内角中至少有两个钝角 |
| C.三个内角都不是钝角 |
| D.三个内角都不是钝角或至少有两个钝角 |
对于任意正整数n,定义“ ”如下:
”如下:
当n是偶数时, ,
,
当n是奇数时,
现在有如下四个命题:
① ;
;
② ;
;
③ 的个位数是0;
的个位数是0;
④ 的个位数是5。
的个位数是5。
其中正确的命题有( )
| A.1个 | B.2个 | C.3个 | D.4个 |
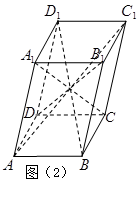
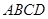 中,有
中,有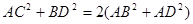 ,那么在图(2)的平行六面体
,那么在图(2)的平行六面体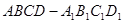 中有
中有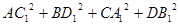 等于( )
等于( )