题目内容
用反证法证明命题“三角形的内角至多有一个钝角”时,假设的内容应为( )
| A.假设至少有一个钝角 | B.假设至少有两个钝角 |
| C.假设没有一个钝角 | D.假设没有一个钝角或至少有两个钝角 |
B
解析试题分析:反证明法的证明步骤:1.假设命题不成立
2.由假设出发,经过推理论证,得出矛盾
3.由矛盾得出假设不成立,从而证明原命题正确
本题中至多有一个钝角的反面是至少有两个是钝角。
考点:反证法的方法及基本步骤

练习册系列答案
相关题目
用数学归纳法证明:“1+a+a2+ +an+1= (a≠1,n∈N*)”在验证n=1时,左端计算所得的项为( )
(a≠1,n∈N*)”在验证n=1时,左端计算所得的项为( )
| A.1 | B.1+a |
| C.1+a+a2 | D.1+a+a2+a3 |
用反证法证明命题“三角形的内角中至多有一个钝角”时,假设正确的是( )
| A.三个内角中至少有一个钝角 |
| B.三个内角中至少有两个钝角 |
| C.三个内角都不是钝角 |
| D.三个内角都不是钝角或至少有两个钝角 |
用反证法证明命题:“若整系数一元二次方程 有有理根,那么
有有理根,那么 中至少有一个是偶数时,下列假设中正确的是
中至少有一个是偶数时,下列假设中正确的是
A.假设 都是偶数 都是偶数 |
B.假设 都不是偶数 都不是偶数 |
C.假设 至多有一个是偶数 至多有一个是偶数 |
D.假设 至多有两个是偶数 至多有两个是偶数 |
用数学归纳法证明1+ +
+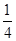 +…+
+…+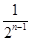 >
>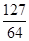 (n∈N*)成立,其初始值至少应取( )
(n∈N*)成立,其初始值至少应取( )
| A.7 | B.8 | C.9 | D.10 |
用数学归纳法证明1+2+3+…+(2n+1)=(n+1)(2n+1)时,从n=k到n=k+1,左边需增添的代数式是( )
| A.2k+2 | B.2k+3 |
| C.2k+1 | D.(2k+2)+(2k+3) |
用反证法证明“a,b,c中至少有一个大于0”,下列假设正确的是( )
| A.假设a,b,c都小于0 |
| B.假设a,b,c都大于0 |
| C.假设a,b,c中都不大于0 |
| D.假设a,b,c中至多有一个大于0 |
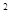 -1︱的值的一个程序
-1︱的值的一个程序