用反证法证明命题“三角形的内角中至多有一个钝角时.假设正确的是A．三个内角中至少有一个钝角B．三个内角中至少有两个钝角C．三个内角都不是钝角D．三个内角都不是钝角或至少有两个钝角题目和参考答案——青夏教育精英家教网—

题目内容

用反证法证明命题“三角形的内角中至多有一个钝角”时，假设正确的是（）

A．三个内角中至少有一个钝角

B．三个内角中至少有两个钝角

C．三个内角都不是钝角

D．三个内角都不是钝角或至少有两个钝角

解析试题分析：反证法的第一步为否定结论，而原题中结论为三角形的内角中至多有一个钝角，即三角形的内角中有一个钝角或没有钝角，显然，其否定为三角形的内角中至少有两个钝角.
考点：反证法.

练习册系列答案

全优计划全能大考卷系列答案

相关题目

有一段演绎推理是这样的：“直线平行于平面，则此直线平行于平面内的所有直线；已知直线平面，直线平面，直线平面，则直线直线”结论显然是错误的，这是因为（）

把正整数按右图所示的规律排序，则从2013到2015的箭头方向依次为（　　）

用反证法证明命题“三角形的内角至多有一个钝角”时，假设正确的是（）

A．假设至少有一个钝角	B．假设至少有两个钝角
C．假设没有一个钝角	D．假设没有一个钝角或至少有两个钝角

用反证法证明命题“三角形的内角至多有一个钝角”时，假设的内容应为（）

A．假设至少有一个钝角	B．假设至少有两个钝角
C．假设没有一个钝角	D．假设没有一个钝角或至少有两个钝角

用火柴棒摆“金鱼”，如图所示：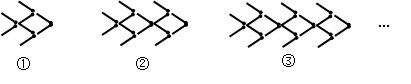

按照上面的规律，第4个“金鱼”图需要火柴棒的根数为

如右图所示，程序框图（算法流程图）的输出结果是．

分析法又称执果索因法，若用分析法证明：“设a>b>c，且a＋b＋c＝0，求证 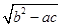<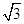a”索的因应是(　　)

A．a－b>0	B．a－c>0
C．(a－b)(a－c)>0	D．(a－b)(a－c)<0

观察下列各式：a+b=1，a²+b²=3，a³+b³=4，a⁴+b⁴=7，a⁵+b⁵=11，…，则a¹⁰+b¹⁰=（　　）

试题分类