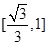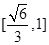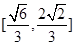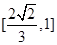设b,c表示两条直线,α,β表示两个平面,则下列命题正确的是( )
| A.若b?α,c∥α,则c∥b |
| B.若b?α,b∥c,则c∥α |
| C.若c?α,α⊥β,则c⊥β |
| D.若c?α,c⊥β,则α⊥β |
已知m和n是两条不同的直线,α和β是两个不重合的平面,那么下面给出的条件中一定能推出m⊥β的是( )
| A.α⊥β,且m?α | B.m∥n,且n⊥β |
| C.α⊥β,且m∥α | D.m⊥n,且n∥β |
若空间中四条直线两两不同的直线 、
、 、
、 、
、 ,满足
,满足 ,
, ,
, ,则下列结论一定正确的是( )
,则下列结论一定正确的是( )
A. | B. |
C. 、 、 既不平行也不垂直 既不平行也不垂直 | D. 、 、 的位置关系不确定 的位置关系不确定 |
如图,在棱长为4的正四面体A-BCD中,M是BC的中点,点P在线段AM上运动(P不与A,M重合),过点P作直线l⊥平面ABC,l与平面BCD交于点Q,给出下列命题:①BC⊥平面AMD;②Q点一定在直线DM上;③VC-AMD=4 .
.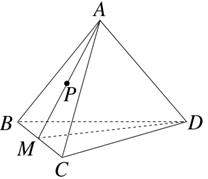
其中正确命题的序号是( )
| A.①② | B.①③ | C.②③ | D.①②③ |
如图,已知六棱锥P-ABCDEF的底面是正六边形,PA⊥平面ABC,PA=2AB,则下列结论正确的是( )
| A.PB⊥AD |
| B.平面PAB⊥平面PBC |
| C.直线BC∥平面PAE |
| D.直线PD与平面ABC所成的角为45° |
如图,在斜三棱柱ABC-A1B1C1中,∠BAC=90°,BC1⊥AC,则C1在底面ABC上的射影H必在( )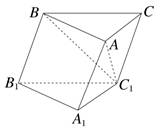
| A.直线AB上 | B.直线BC上 |
| C.直线AC上 | D.△ABC内部 |
设m,n是两条不同的直线,α,β,γ是三个不同的平面,有下列四个命题:
①若m?β,α⊥β,则m⊥α;②若α∥β,m?α,则m∥β;③若n⊥α,n⊥β,m⊥α,则m⊥β;④若α⊥γ,β⊥γ,m⊥α,则m⊥β.
其中正确命题的序号是( )
| A.①③ | B.①② | C.③④ | D.②③ |
已知两条直线m,n,两个平面α,β.给出下面四个命题:
①m∥n,m⊥α⇒n⊥α;
②α∥β,m?α,n?β⇒m∥n;
③m∥n,m∥α⇒n∥α;
④α∥β,m∥n,m⊥α⇒n⊥β.
其中正确命题的序号是( )
| A.①③ | B.②④ | C.①④ | D.②③ |
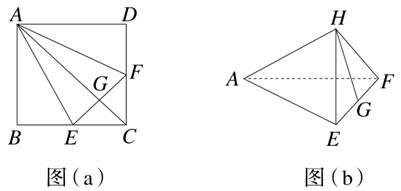
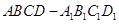 中,点
中,点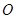 为线段
为线段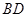 的中点.设点
的中点.设点 在线段
在线段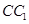 上,直线
上,直线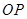 与平面
与平面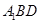 所成的角为
所成的角为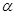 ,则
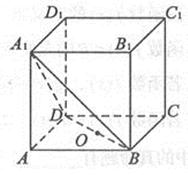
,则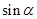 的取值范围是( )
的取值范围是( )