设 ,若直线
,若直线 与
与 轴相交于点
轴相交于点 ,与
,与 轴相交于点
轴相交于点 ,且坐标原点
,且坐标原点 到直线
到直线 的距离为
的距离为 ,则
,则 的面积
的面积 的最小值为
的最小值为
A.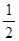 | B.2 | C.3 | D.4 |
若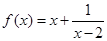
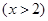 在
在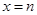 处取得最小值,则
处取得最小值,则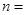 ( )
( )
A.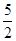 | B.3 | C.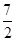 | D.4 |
下列结论正确的是( )
①“ ”是“对任意的正数
”是“对任意的正数 ,均有
,均有 ”的充分非必要条件
”的充分非必要条件
②随机变量 服从正态分布
服从正态分布 ,则
,则
③线性回归直线至少经过样本点中的一个
④若10名工人某天生产同一零件,生产的件数是15,17,14,10,15,17,17,16,14,12,设其
平均数为 ,中位数为
,中位数为 ,众数为
,众数为 ,则有
,则有

| A.③④ | B.①② | C.①③④ | D.①④ |
直线 恒过定点
恒过定点 ,且点
,且点 在直线
在直线 (
( )上,则
)上,则 的最小值为
的最小值为
A. | B. | C. | D. |
半径为2的球面上有A,B,C,D四点,且AB,AC,AD两两垂直,则三个三角形面积之和 的最大值为( )
的最大值为( )
| A.4 | B.8 | C.16 | D.32 |
“a>b>0”是“ab< ”的 ( )
”的 ( )
| A.充分而不必要条件 | B.必要而不充分条件 |
| C.充分必要条件 | D.既不充分也不必要条件 |
在直角坐标系中,定义两点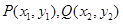 之间的“直角距离”为
之间的“直角距离”为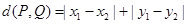 ,
,
现给出四个命题:
①已知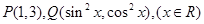 ,则
,则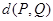 为定值;
为定值;
②用 表示
表示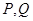 两点间的“直线距离”,那么
两点间的“直线距离”,那么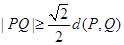 ;
;
③已知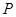 为直线
为直线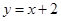 上任一点,
上任一点,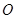 为坐标原点,则
为坐标原点,则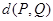 的最小值为
的最小值为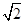 ;
;
④已知 三点不共线,则必有
三点不共线,则必有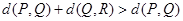 .
.
| A.②③ | B.①④ | C.①② | D.①②④ |
设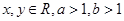 ,若
,若 ,则
,则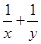 的最大值为( )
的最大值为( )
| A.2 | B.3 | C.4 | D.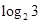 |
已知 与
与 互为反函数,若
互为反函数,若 恒成立,则实数
恒成立,则实数 的取值范围为( )
的取值范围为( )
A. | B. | C. | D. |
 ,得2分的概率为
,得2分的概率为 ,不得分的概率为
,不得分的概率为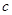 ,
, ,已知他投篮一次得分的期望是2,则
,已知他投篮一次得分的期望是2,则 的最小值为( )
的最小值为( )


