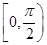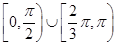设函数y=f(x),x∈R的导函数为 ,且
,且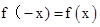 ,
, ,则下列成立的是( )
,则下列成立的是( )
| A.f(0)<e?1f(1)<e2f(2) | B.e2f(2)< f(0)<e?1f(1) |
| C.e2f(2)<e?1f(1)<f(0) | D.e?1f(1)<f(0)<e2f(2) |
已知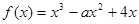 有两个极值点
有两个极值点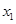 、
、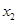 ,且
,且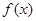 在区间(0,1)上有极大值,无极小值,则实数
在区间(0,1)上有极大值,无极小值,则实数 的取值范围是( )
的取值范围是( )
A.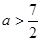 | B.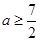 | C.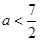 | D.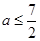 |
曲线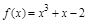 上点
上点 处的切线垂直于直线
处的切线垂直于直线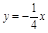 ,则点P0的坐标是( )
,则点P0的坐标是( )
A.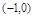 | B.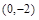 | C.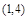 | D.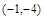 或 或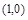 |
已知 是定义在
是定义在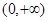 上的非负可导函数,且满足
上的非负可导函数,且满足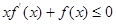 .对任意正数
.对任意正数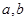 ,若
,若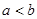 ,则必有( )
,则必有( )
A.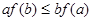 | B.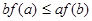 |
C.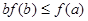 | D.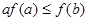 |
已知函数 有极大值和极小值,则实数
有极大值和极小值,则实数 的取值范围是 ( )
的取值范围是 ( )
A.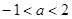 | B.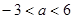 |
C.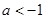 或 或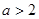 | D.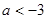 或 或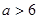 |
曲线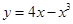 在点
在点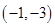 处的切线方程是( )
处的切线方程是( )
A.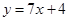 | B.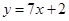 | C.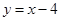 | D. |
对于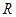 上可导的任意函数
上可导的任意函数 ,若满足
,若满足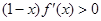 ,则必有 ( )
,则必有 ( )
A.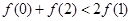 | B.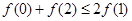 |
C.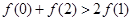 | D.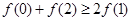 |
已知 ,则
,则 = ( )
= ( )
A. | B. |
C. | D. |
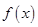 、
、 分别是定义在R上的奇函数和偶函数。当
分别是定义在R上的奇函数和偶函数。当 时,
时,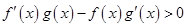 且
且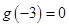 。则不等式
。则不等式 的解集是( )
的解集是( )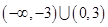


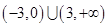
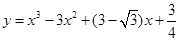 上移动,经过点P的切线的倾斜角为
上移动,经过点P的切线的倾斜角为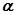 ,则角
,则角