题目内容
设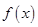 、
、 分别是定义在R上的奇函数和偶函数。当
分别是定义在R上的奇函数和偶函数。当 时,
时,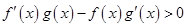 且
且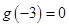 。则不等式
。则不等式 的解集是( )
的解集是( )
A.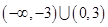 | B. |
C. | D.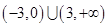 |
D
解析试题分析: ,函数
,函数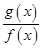 在
在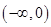 上是减函数,
上是减函数,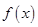 、
、 分别是定义在R上的奇函数和偶函数,所以函数
分别是定义在R上的奇函数和偶函数,所以函数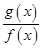 是奇函数,在
是奇函数,在 上是减函数,
上是减函数,
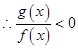 的解为
的解为 或
或
考点:函数导数与单调性及数形结合法
点评:本题综合考查了函数的单调性奇偶性及函数图像等性质,具有一定的综合性,求解本题的入手点在由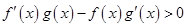 构造新函数
构造新函数

练习册系列答案
相关题目
已知函数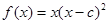 在
在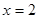 处有极大值,则
处有极大值,则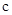 =( )
=( )
| A.6 | B.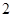 | C.2或6 | D.-2或6 |
设 分别是定义在R上的奇函数和偶函数,当
分别是定义在R上的奇函数和偶函数,当 时,
时, ,且g(-3)=0,则不等式
,且g(-3)=0,则不等式 的解集是 ( )
的解集是 ( )
| A.(-3,0)∪(3,+∞) | B. (-3,0)∪(0,3) |
| C.(-∞,-3)∪(3,+∞) | D.(-∞,-3)∪(0,3) |
曲线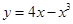 在点
在点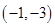 处的切线方程是( )
处的切线方程是( )
A.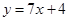 | B.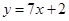 | C.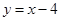 | D. |
若 ,则
,则 等于( )
等于( )
A. | B. | C.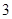 | D. |
设 ,则二项式
,则二项式 的展开式中
的展开式中 项的系数为( )
项的系数为( )
| A.-192 | B.193 | C.-6 | D.7 |
函数 导数是( )
导数是( )
A. | B. |
C.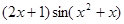 | D. |
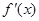 是函数f(x)的导函数,如果
是函数f(x)的导函数,如果
 ,那么曲线f(x)上任一点处的切线的倾斜角
,那么曲线f(x)上任一点处的切线的倾斜角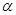 的取值范围是
的取值范围是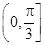

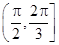

 为
为 ,那么,原油温度的瞬时变化率的最小值是( )
,那么,原油温度的瞬时变化率的最小值是( )

