某市一家庭今年一月份、二月份、和三月份煤气用量和支付费用如下表所示:
| 月份 | 用气量(立方米) | 煤气费(元) |
| 1 | 4 | 4.00 |
| 2 | 25 | 14.00 |
| 3 | 35 | 19.00 |
若每月用气量不超过最低额度
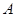
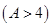 立方米时,只付基本费3元+每户每月定额保险费
立方米时,只付基本费3元+每户每月定额保险费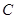
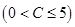 元;若用气量超过
元;若用气量超过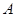 立方米时,超过部分每立方米付
立方米时,超过部分每立方米付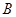 元.
元.⑴根据上面的表格求
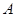 、
、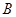 、
、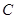 的值;
的值;⑵若用户第四月份用气30立方米,则应交煤气费多少元?
某市一家庭今年一月份、二月份、和三月份煤气用量和支付费用如下表所示:
| 月份 | 用气量(立方米) | 煤气费(元) |
| 1 | 4 | 4.00 |
| 2 | 25 | 14.00 |
| 3 | 35 | 19.00 |
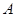
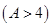 立方米时,只付基本费3元+每户每月定额保险费
立方米时,只付基本费3元+每户每月定额保险费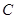
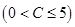 元;若用气量超过
元;若用气量超过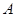 立方米时,超过部分每立方米付
立方米时,超过部分每立方米付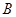 元.
元.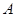 、
、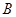 、
、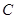 的值;
的值;