题目内容
设 为实数,记函数
为实数,记函数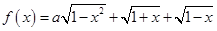 的最大值为
的最大值为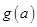 .
.
(1)设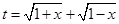 ,求
,求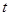 的取值范围,并把
的取值范围,并把 表示为
表示为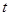 的函数
的函数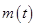 ;
;
(2)求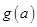 .
.
(Ⅰ)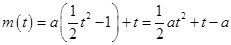
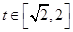 ;(Ⅱ)
;(Ⅱ)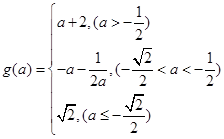
解析试题分析:观察到 与
与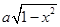 是有关联的,平方后就可以看出彼此之间的关联.这样
是有关联的,平方后就可以看出彼此之间的关联.这样 就可以化成以t为自变量的函数.那么第二问就转化成了带参数的二次函数的最值问题.根据对称轴进行分类讨论即可.
就可以化成以t为自变量的函数.那么第二问就转化成了带参数的二次函数的最值问题.根据对称轴进行分类讨论即可.
试题解析:(1)因为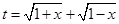 ,
,
所以要使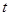 有意义,必须
有意义,必须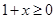 且
且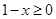 ,即
,即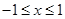
因为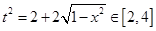 ,且
,且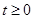 ①
①
所以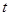 得取值范围是
得取值范围是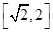
由①得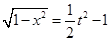
所以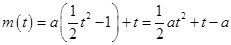 ,
,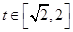 ; 2分
; 2分
(2)由题意知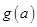 即为函数
即为函数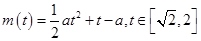 的最大值.
的最大值.
因为直线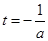 是抛物线
是抛物线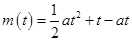 的对称轴,
的对称轴,
所以可分以下几种情况进行讨论:
当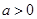 时函数
时函数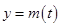 ,
,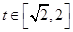 的图像是开口向上的抛物线的一段,
的图像是开口向上的抛物线的一段,
由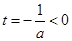 知
知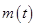 在
在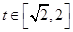 上单调递增,故
上单调递增,故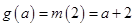 ; 4分
; 4分
②当 时,
时,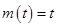 ,
,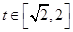 ,有
,有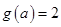 ; 6分
; 6分
③当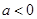 时,函数
时,函数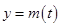 ,
,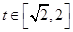 的图像是开口向下的抛物线的一段,
的图像是开口向下的抛物线的一段,
若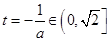 ,即
,即 时,
时,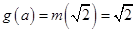 ,
,
若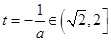 ,即
,即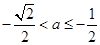 时,
时,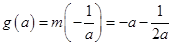 ,
,
若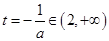 ,即
,即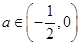 时,
时,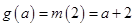 9分
9分
综上,有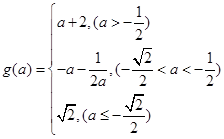 10分
10分
考点:含参数的二次函数最值的求法.

练习册系列答案
相关题目
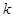 米的圆.在这个圆上安装座位,且每个座位和圆心处的支点都有一根直的钢管相连.经预算,摩天轮上的每个座位与支点相连的钢管的费用为
米的圆.在这个圆上安装座位,且每个座位和圆心处的支点都有一根直的钢管相连.经预算,摩天轮上的每个座位与支点相连的钢管的费用为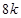 元/根,且当两相邻的座位之间的圆弧长为
元/根,且当两相邻的座位之间的圆弧长为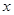 米时,相邻两座位之间的钢管和其中一个座位的总费用为
米时,相邻两座位之间的钢管和其中一个座位的总费用为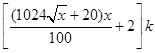 元.假设座位等距离分布,且至少有两个座位,所有座位都视为点,且不考虑其他因素,记摩天轮的总造价为
元.假设座位等距离分布,且至少有两个座位,所有座位都视为点,且不考虑其他因素,记摩天轮的总造价为 元.
元.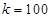 米时,试确定座位的个数,使得总造价最低?
米时,试确定座位的个数,使得总造价最低?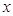 千件,需另投入成本为
千件,需另投入成本为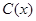 (万元),当年产量不足80千件时,
(万元),当年产量不足80千件时,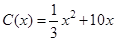 (万元).当年产量不小于80千件时,
(万元).当年产量不小于80千件时,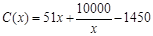 (万元).每件商品售价为500元.通过市场分析,该厂生产的商品能全部售完.
(万元).每件商品售价为500元.通过市场分析,该厂生产的商品能全部售完.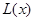 (万元)关于年产量
(万元)关于年产量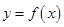 和
和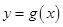 的图象关于
的图象关于 轴对称,且
轴对称,且 .
.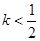 时,解不等式
时,解不等式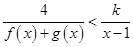 .
.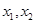 是关于
是关于 的方程
的方程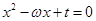 的两个根,且
的两个根,且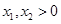 .
.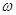 与
与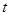 之间满足的关系式;
之间满足的关系式;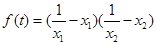 ,若存在
,若存在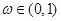 ,使不等式
,使不等式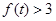 在其定义域范围内恒成立,求
在其定义域范围内恒成立,求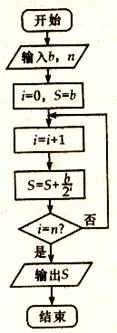
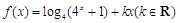 是偶函数.
是偶函数.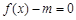 有解,求m的取值范围.
有解,求m的取值范围.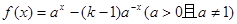 是定义域为
是定义域为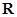 的奇函数.
的奇函数.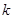 的值;
的值;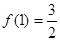 ,且
,且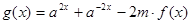 在
在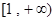 上的最小值为
上的最小值为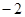 ,求
,求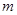 的值.
的值.