题目内容
已知函数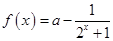 .
.
(1)求证不论 为何实数,
为何实数, 总是增函数;
总是增函数;
(2)确定 的值,使
的值,使 为奇函数;
为奇函数;
(3)当 为奇函数时,求
为奇函数时,求 的值域.
的值域.
(Ⅰ)见下(Ⅱ)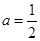 (Ⅲ)
(Ⅲ)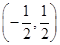
解析试题分析:(1)函数的单调性的证明有两种基本的方法.一是定义法;而是利用导数.在目前阶段,我们只能用定义来证明函数的单调性.即分三个步骤:①设值②作差③比较差值与0的关系.(2)作为奇函数,满足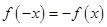 ,可求得
,可求得 的值.(Ⅲ)求函数的值域,根据函数解析式的特点,有各种不同的方法,一般有直接观察法、换元法、单调性法、判别式法、图像法等.本题中函数值域的求得较为简单,用直接观察法即可.
的值.(Ⅲ)求函数的值域,根据函数解析式的特点,有各种不同的方法,一般有直接观察法、换元法、单调性法、判别式法、图像法等.本题中函数值域的求得较为简单,用直接观察法即可.
试题解析(1)∵ 的定义域为R,任取
的定义域为R,任取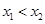
则
∵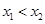 ∴
∴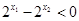 ,
,
∴ 即
即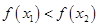
∴不论 为何实数
为何实数 总为增函数, 6分
总为增函数, 6分
(2)∵ 为奇函数,∴
为奇函数,∴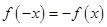
即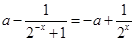 解得
解得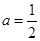 8分
8分
(3)由(2)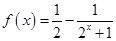
∵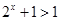 ∴
∴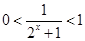 ∴
∴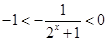
∴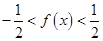
∴ 的值域为
的值域为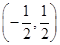 12分
12分
考点:函数的奇偶性、增减性和值域.

练习册系列答案
相关题目
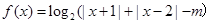 .
. 时,求函数
时,求函数 的定义域;
的定义域; 的不等式
的不等式 的解集是
的解集是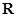 ,求
,求 的取值范围.
的取值范围.
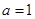 时,求函数
时,求函数 在
在 的值域;
的值域;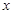 的方程
的方程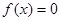 有解,求
有解,求 的取值范围.
的取值范围. 若存在
若存在 ,使得
,使得 成立,则称
成立,则称 为
为
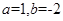 时,求函数
时,求函数 的不动点;
的不动点; ,函数
,函数 的取值范围;
的取值范围; 图象上
图象上 、
、 两点的横坐标是函数
两点的横坐标是函数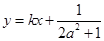 对称,求
对称,求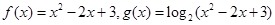 ,且两函数定义域均为
,且两函数定义域均为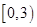 ,
, 在定义域内的图像,并求
在定义域内的图像,并求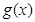 的值域.(5分)
的值域.(5分)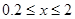 时,排水量V是垃圾杂物密度x的一次函数。
时,排水量V是垃圾杂物密度x的一次函数。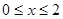 时,求函数V(x)的表达式;
时,求函数V(x)的表达式; 可以达到最大,求出这个最大值。
可以达到最大,求出这个最大值。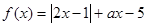 (a是常数,a∈R)
(a是常数,a∈R)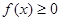 的解集;
的解集;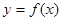 恰有两个不同的零点,求a的取值范围.
恰有两个不同的零点,求a的取值范围. 千件,并且全部销售完,每千件的销售收入为
千件,并且全部销售完,每千件的销售收入为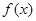 万元,且
万元,且
 (万元)关于年产品
(万元)关于年产品 (
( ).
). 的定义域和值域均是
的定义域和值域均是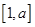 ,求实数
,求实数 的值;
的值; 上是减函数,且对任意的
上是减函数,且对任意的 ,
,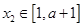 ,总有
,总有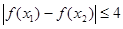 ,求实数
,求实数