幂指函数
在求导时，可运用对数法：在函数解析式两边求对数得
，两边同时求导得
，于是
。运用此方法可以探求得知
的一个单调递增区间为（ ）
| A．(0,2) | B．(2,3) | C．(e,4) | D．(3,8) |
定义在
上的函数
；当
时，
，若
，
，则
的大小关系为（ ）
A． | B． | C． | D． |
已知幂函数
是定义在区间
上的奇函数，则
（ ）
| A．8 | B．4 | C．2 | D．1 |
恒过定点（ ）
A． | B．  | C． | D． |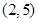
，则函数
的大致图像是( )
已知：
在
上为减函数，则
的取值范围为（ ）。
A． | B． | C． | D． |
已知定义在
上的函数
满足
，且
，若有穷数列
（
）的前
项和等于
，则等于（ ）
| A．4 | B．6 | C．5 | D．7 |
对任意
，函数
不存在极值点的充要条件是（ ）
A． 或 | B． |
C． | D． 或 |
的图像大致形状是（ ）
若
（其中
），则函数
的图象( ）
| A．关于y轴对称 | B．关于X轴对称 |
| C．关于直线y=x轴称 | D．关于原点对称 |