题目内容
已知: 在
在 上为减函数,则
上为减函数,则 的取值范围为( )。
的取值范围为( )。
A. | B. | C. | D. |
C
解析试题分析:因为 ,所以令
,所以令 ,则
,则 ,
,
当0<a<1,时, 是单调递减的,
是单调递减的, 是单调递减的,所以
是单调递减的,所以 是单调递增的,此时不满足题意;
是单调递增的,此时不满足题意;
当a>1时, 是单调递减的,
是单调递减的, 是单调递增的,所以
是单调递增的,所以 是单调递减的,又由
是单调递减的,又由  >0得
>0得 ,所以
,所以 ,即
,即 ,所以
,所以 。
。
综上知:a的范围为 。
。
考点:对数函数的定义域;对数函数的单调性;复合函数的单调性。
点评:此题考查的是复合函数单调性的判断。对于复合函数的判断我们只需要掌握四个字:同增异减。同时,本题也是一个易错题,错误的主要原因为忽略了定义域的限制。因为

练习册系列答案
 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案
相关题目
 满足
满足 ,下列不等式中正确的是( )
,下列不等式中正确的是( )
A. | B. | C. | D. |
函数 的零点所在的大致区间是( )
的零点所在的大致区间是( )
A. | B. | C. 和 和 | D. |
已知定义在R上的奇函数 ,满足
,满足 ,且在区间[0,2]上是减函数,则( )
,且在区间[0,2]上是减函数,则( )
A. | B. |
C. | D. |
函数 在
在 上恒为正数,则实数
上恒为正数,则实数 的取值范围是( )
的取值范围是( )
A. | B. | C. | D. |
幂指函数 在求导时,可运用对数法:在函数解析式两边求对数得
在求导时,可运用对数法:在函数解析式两边求对数得 ,两边同时求导得
,两边同时求导得 ,于是
,于是 。运用此方法可以探求得知
。运用此方法可以探求得知 的一个单调递增区间为( )
的一个单调递增区间为( )
| A.(0,2) | B.(2,3) | C.(e,4) | D.(3,8) |
函数 的图像与
的图像与 轴的交点个数为 ( )
轴的交点个数为 ( )
| A.一个 | B.至少一个 | C.至多两个 | D.至多一个 |
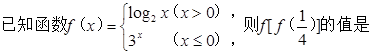 ( )
( )
A. | B.9 | C. | D.-9 |
定义在R上的任意函数f (x)都可以表示成一个奇函数g (x)和一个偶函数h (x)之和,如果f (x)=lg(10x+1),x∈R.那么
| A.g (x)=x,h (x)=lg(10x+10-x+1) |
B.g (x)= ,h (x)= ,h (x)= |
C.g (x)= ,h (x)=lg(10x+1)- ,h (x)=lg(10x+1)- |
D.g (x)=- ,h (x)= ,h (x)= |