题目内容
已知定义在 上的函数
上的函数 满足
满足 ,且
,且
 ,若有穷数列
,若有穷数列 (
( )的前
)的前 项和等于
项和等于 ,则
,则 等于( )
等于( )
| A.4 | B.6 | C.5 | D.7 |
C
解析试题分析:令
 ,因为
,因为 ,则
,则
 ,所以
,所以 在R上是单调递减的,所以0<a<1,因为
在R上是单调递减的,所以0<a<1,因为 ,所以
,所以 或 a=2(舍去)。
或 a=2(舍去)。
所以有穷数列 (
( )是以
)是以 为首项,
为首项, 为公比的等比数列,因为有穷数列
为公比的等比数列,因为有穷数列 (
( )的前
)的前 项和等于
项和等于 ,所以
,所以 ,解
,解 。
。
考点:指数函数的性质;导数的运算公式及运算法则;利用导数研究函数的单调性;数列的前n项和;无穷数列的前n项和公式。
点评:本题考查数列与函数的综合,考查导数知识的运用。其难点为构造函数 =
=  ,且判断出
,且判断出 在R上是单调递减的。确定有穷数列
在R上是单调递减的。确定有穷数列 (
( )是以
)是以 为首项,
为首项, 为公比的等比数列是关键.此题属于较难题目。
为公比的等比数列是关键.此题属于较难题目。

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
一元二次方程 有一个正根和一个负根的充分不必要条件是:( )
有一个正根和一个负根的充分不必要条件是:( )
A. | B. | C. | D. |
若函数 与
与 的图象有交点,则
的图象有交点,则 的取值范围是( )
的取值范围是( )
A. 或 或  | B. |
C. | D. |
对实数a和b,定义运算“?”:a?b= ,设函数f(x)=(x2-2)?(x-x2),x∈R,若函数y=f(x)-c的图象与x轴恰有两个公共点,则实数c的取值范围是
,设函数f(x)=(x2-2)?(x-x2),x∈R,若函数y=f(x)-c的图象与x轴恰有两个公共点,则实数c的取值范围是
A.(-∞,-2]∪ | B. |
C. | D.(-∞,-2]∪ |
已知 ,
, ,则
,则 ( )
( )
| A.3 | B.8 | C.4 | D. |
定义在 上的函数
上的函数 ;当
;当 时,
时, ,若
,若 ,
, ,则
,则 的大小关系为( )
的大小关系为( )
A. | B. | C. | D. |
若二次函数 的部分图像如右图所示,则函数
的部分图像如右图所示,则函数 的零点所在的区间是( )
的零点所在的区间是( )
A. | B.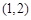 | C. | D. |
已知 ,那么
,那么 用
用 表示是( )
表示是( )
A.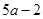 | B. | C. | D. |
函数f (x)=(m2-m-1)x 是幂函数,且在x∈(0,+∞)上是减函数,那么实数
是幂函数,且在x∈(0,+∞)上是减函数,那么实数
m的值为
A. | B.-2 | C. | D.2 |