题目内容
定义在
上的函数
；当
时，
，若
，
，则
的大小关系为（ ）
A． | B． | C． | D． |
B
解析试题分析：由题意可知
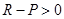因为当时，，所以
,所以
,同理可判断
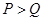,所以.
考点：本小题主要考查新定义下比较大小问题，考查学生转化问题的能力和推理论证能力.
点评：比较大小问题首先想到的是作差或作商.
练习册系列答案
相关题目
大西洋鲑鱼每年都要逆流而上游回产地产卵.经研究发现：鲑鱼的游速v(单位：m/s)与耗氧量的单位数
的函数关系式为：
。若某条鱼想把游速提高1 m/s，它的耗氧量将增大到原来的a倍，则a=
| A．9 | B．8 | C．3 | D．2 |
已知函数
则
的值为（ ）
| A．4 | B．6 | C．8 | D．11 |
设
，则
的大小关系是( )
| A．a>c>b | B．a>b>c |
| C．c>a>b | D．b>c>a |
已知定义在
上的函数
满足
，且
，若有穷数列
（
）的前
项和等于
，则等于（ ）
| A．4 | B．6 | C．5 | D．7 |
已知函数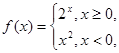
则
（ ）
| A．16 | B． | C．4 | D． |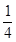
，函数
与
的图像可能是（ ）
函数
与
的图象（ ）
| A．关于原点对称 | B．关于 轴对称 |
C．关于 轴对称. | D．关于 对称 |
若函数
，则
的值为（ ）
A． | B． | C． | D． |