函数 的定义域为
的定义域为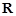 ,
, ,对任意
,对任意 ,
, ,则
,则 的解集为:
的解集为:
A.( ,+ ,+ ) ) | B.( ,1) ,1) |
C.( , , ) ) | D.( ,+ ,+ ) ) |
已知函数 的图像与
的图像与 轴恰有两个公共点,则
轴恰有两个公共点,则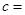
A. 或2 或2 | B. 或3 或3 | C. 或1 或1 | D. 或1 或1 |
已知函数 ,则
,则 ( )
( )
| A.-2 | B.10 | C.2 | D.-10 |
函数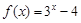 的零点所在区间为( )
的零点所在区间为( )
A.( 1,0) 1,0) | B.(0,1) | C.(1,2) | D.(2,3) |
下列函数中,在区间 上是增函数的是 ( )
上是增函数的是 ( )
A. | B. | C. | D. |
已知 ,若函数
,若函数 ,则
,则 的
的
根的个数最多有( )
| A.1个 | B.2个 | C.3个 | D.4个 |
已知 为
为 上的减函数,则满足
上的减函数,则满足 的实数
的实数 的取值范围是( )
的取值范围是( )
A. | B.(0,1) | C. | D. |
给定方程: ,下列命题中:(1) 该方程没有小于0的实数解;(2) 该方程有无数个实数解;(3) 该方程在(–∞,0)内有且只有一个实数解;
,下列命题中:(1) 该方程没有小于0的实数解;(2) 该方程有无数个实数解;(3) 该方程在(–∞,0)内有且只有一个实数解;
(4) 若x0是该方程的实数解,则x0>–1.
则正确命题的个数是 ( )
| A.1 | B.2 | C.3 | D.4 |
定义域是一切实数的函数 ,其图像是连续不断的,且存在常数
,其图像是连续不断的,且存在常数 (
( )
)
使得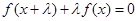 对任意实数
对任意实数 都成立,则称
都成立,则称 是一个“
是一个“ —伴随函数”. 有
—伴随函数”. 有
下列关于“ —伴随函数”的结论:
—伴随函数”的结论:
① 是常数函数中唯一一个“
是常数函数中唯一一个“ —伴随函数”;
—伴随函数”;
②“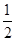 —伴随函数”至少有一个零点;
—伴随函数”至少有一个零点;
③ 是一个“
是一个“ —伴随函数”;
—伴随函数”;
其中正确结论的个数是 ( )
| A.1个; | B.2个; | C.3个; | D.0个; |
 的图像如左图所示,则函数
的图像如左图所示,则函数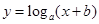 的图像可能是( )
的图像可能是( )