题目内容
函数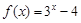 的零点所在区间为( )
的零点所在区间为( )
A.( 1,0) 1,0) | B.(0,1) | C.(1,2) | D.(2,3) |
C
解析试题分析:依次将区间端点代入函数,可知 ,根据函数的零点存在定理可知该函数的零点在区间(1,2)中.
,根据函数的零点存在定理可知该函数的零点在区间(1,2)中.
考点:本小题主要考查函数的零点存在定理的应用.
点评:函数的零点存在定理可以包保证在该区间内有零点,但是有几个零点不确定.

练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
下列式子正确的是( )
A. | B. | C. | D. |
函数 和
和 的递增区间依次是( )
的递增区间依次是( )
A.(-∞,0 ,(-∞,1 ,(-∞,1 | B.(-∞,0 ,[1,+∞ ,[1,+∞ |
C.[0,+∞ ,(-∞,1 ,(-∞,1 | D.[0,+∞),[1,+∞) |
定义域是一切实数的函数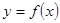 ,其图像是连续不断的,且存在常数
,其图像是连续不断的,且存在常数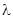 (
(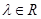 )使得
)使得  对任意实数
对任意实数 都成立,则称
都成立,则称 是一个“
是一个“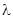 —伴随函数”.有下列关于“
—伴随函数”.有下列关于“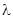 —伴随函数”的结论:
—伴随函数”的结论:
① 是常数函数中唯一一个“
是常数函数中唯一一个“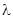 —伴随函数”;
—伴随函数”;
②“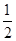 —伴随函数”至少有一个零点;
—伴随函数”至少有一个零点;
③ 是一个“
是一个“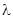 —伴随函数”;
—伴随函数”;
其中正确结论的个数是 ( )
| A.1个; | B.2个; | C.3个; | D.0个; |
定义域是一切实数的函数 ,其图像是连续不断的,且存在常数
,其图像是连续不断的,且存在常数 (
( )
)
使得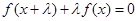 对任意实数
对任意实数 都成立,则称
都成立,则称 是一个“
是一个“ —伴随函数”. 有
—伴随函数”. 有
下列关于“ —伴随函数”的结论:
—伴随函数”的结论:
① 是常数函数中唯一一个“
是常数函数中唯一一个“ —伴随函数”;
—伴随函数”;
②“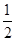 —伴随函数”至少有一个零点;
—伴随函数”至少有一个零点;
③ 是一个“
是一个“ —伴随函数”;
—伴随函数”;
其中正确结论的个数是 ( )
| A.1个; | B.2个; | C.3个; | D.0个; |
已知函数 ,若
,若 ,则
,则 等于 ( )
等于 ( )
A. | B. | C. | D. |
已知a>b,二次三项式ax2 +2x +b≥0对于一切实数x恒成立,又 ,使
,使 成立,则
成立,则 的最小值为( )
的最小值为( )
| A.1 | B. | C.2 | D.2 |
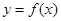 在区间
在区间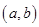 的导函数为
的导函数为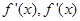 在区间
在区间 若在区间
若在区间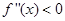 恒成立,则称函数
恒成立,则称函数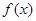 在区间
在区间 ,若对任意的实数m满足
,若对任意的实数m满足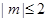 时,函数
时,函数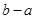 的最大值为( )
的最大值为( ) 的图象大致是
的图象大致是