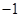定义在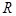 上的函数
上的函数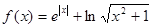 ,且
,且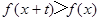 在
在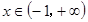 上恒成立,则关于
上恒成立,则关于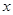 的方程
的方程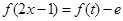 的根的个数叙述正确的是( ).
的根的个数叙述正确的是( ).
| A.有两个 | B.有一个 | C.没有 | D.上述情况都有可能 |
设f(x),g(x)分别是定义在R上的奇函数和偶函数,当x<0时, ,且
,且 ,则不等式
,则不等式 的解集是( )
的解集是( )
| A.(-3,0)∪(3,+∞) | B.(-3,0)∪(0,3) |
| C.(-∞,-3)∪(3,+∞) | D.(-∞,-3)∪(0,3) |
设f(x),g(x)分别是定义在R上的奇函数和偶函数,当x<0时, ,且
,且 ,则不等式
,则不等式 的解集是( )
的解集是( )
| A.(-3,0)∪(3,+∞) | B.(-3,0)∪(0,3) |
| C.(-∞,-3)∪(3,+∞) | D.(-∞,-3)∪(0,3) |
在给定映射 即
即
 的条件下,与B中元素
的条件下,与B中元素 对应的A中元素是( )
对应的A中元素是( )
A. | B. 或 或 |
C. | D. 或 或 |
已知函数 为奇函数,且当
为奇函数,且当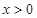 时
时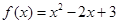 ,则当
,则当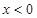 时,
时, 的解析式( )
的解析式( )
A.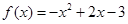 | B.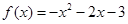 |
C.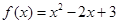 | D.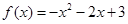 |
偶函数 在区间[0,4]上单调递减,则有( )
在区间[0,4]上单调递减,则有( )
A. |
B. |
C. |
D. |
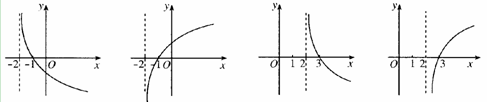
 的图像可能是( )
的图像可能是( ) 




 上的奇函数,若对于任意的实数
上的奇函数,若对于任意的实数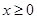 ,都有
,都有 ,且当
,且当 时,
时, ,则
,则 的值为( )
的值为( )