题目内容
若函数f(x)=(k-1)ax-a-x(a>0,且a≠1)在R上既是奇函数,又是减函数,则g(x)=loga(x+k)的图象是( )
A. B. C. D.
A
解析试题分析:由已知 ,则有
,则有 ,所以
,所以 ,则
,则 ,
,
又函数 是减函数,则
是减函数,则 ,所以
,所以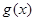 的图象为A.
的图象为A.
考点:1、函数的奇偶性;2、函数的单调性;3、函数图象以及变换.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
函数 的定义域为( )
的定义域为( )
A. | B. |
C. | D. |
已知函数 若a、b、c互不相等,且
若a、b、c互不相等,且 ,则a+b+c的取值范围是( )
,则a+b+c的取值范围是( )
| A.(1,2014) | B.(1,2015) | C.(2,2015) | D.[2,2015] |
函数图象和方程的曲线有密切的关系,如把抛物线 的图象绕远点沿逆时针方向旋转
的图象绕远点沿逆时针方向旋转 就得到函数
就得到函数 的图象,若把双曲线
的图象,若把双曲线 的图象绕原点逆时针方向旋转一定的角度
的图象绕原点逆时针方向旋转一定的角度 后,就得到某一函数的图象,则旋转角
后,就得到某一函数的图象,则旋转角 可以是( )
可以是( )
A. | B. | C. | D. |
已知函数 为奇函数,且当
为奇函数,且当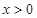 时
时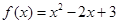 ,则当
,则当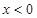 时,
时, 的解析式( )
的解析式( )
A.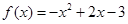 | B.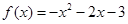 |
C.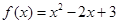 | D.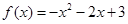 |
定义在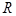 上的函数
上的函数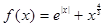 ,且
,且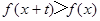 在
在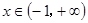 上恒成立,则关于
上恒成立,则关于 的方程
的方程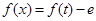 的根的个数叙述正确的是( )
的根的个数叙述正确的是( )
| A.有两个 | B.有一个 | C.没有 | D.上述情况都有可能 |
下列各项表示相等函数的是( )
A. | B. |
C. | D. |
下列函数中,在其定义域内既是奇函数又是减函数的是( )
A.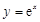 | B.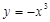 | C.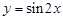 | D.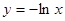 |
 且
且 ,函数
,函数 在同一坐标系中的图象可能是( )
在同一坐标系中的图象可能是( )