已知f(x)是定义在实数集R上的增函数,且f(1)=0,函数g(x)在(-∞,1]上为增函数,在[1,+∞)上为减函数,且g(4)=g(0)=0,则集合{x|f(x)g(x)≥0}等于( )
| A．{x|x≤0或1≤x≤4} |
| B．{x|0≤x≤4} |
| C．{x|x≤4} |
| D．{x|0≤x≤1或x≥4} |
下列函数中,既是偶函数,又在区间(0,+∞)上单调递减的函数是( )
| A．y=x-2 | B．y=x-1 |
| C．y=x2 | D．y= |
已知函数f(x)是定义在R上的偶函数,且在区间[0,+∞)上单调递增.若实数a满足f(log2a)+f(
a)≤2f(1),则a的取值范围是( )
| A．[1,2] | B． | C． | D．(0,2] |
已知函数f(x)为奇函数,且当x>0时,f(x)=x2+
,则f(-1)等于( )
| A．2 | B．1 | C．0 | D．-2 |
给定函数①y=
,②y=(x+1),③y=|x-1|,④y=2x+1,其中在区间(0,1)上单调递减的函数的序号是( )
| A．①② | B．②③ |
| C．③④ | D．①④ |
下列函数中,既是奇函数又是增函数的为( )
| A．y=x+1 | B．y=-x3 |
| C．y= | D．y=x|x| |
下列函数中,既是偶函数又在区间(0,+∞)上单调递减的是( )
| A．y= | B．y=e-x |
| C．y=-x2+1 | D．y=lg|x| |
设
是
上的奇函数，且
时，
，对任意
，不等式
恒成立，则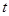
的取值范围（ ）
A． | B． | C． | D． |
关于
的方程：
有两个实数根，则实数
的取值范围（ ）
A． | B． | C． | D． |
函数
的一个零点所在的区间是（ ）
A． | B． | C． | D． |