题目内容
(本小题满分14分)已知椭圆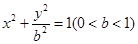 的左焦点为F,左右顶点分别为A,C上顶点为B,过F,B,C三点作
的左焦点为F,左右顶点分别为A,C上顶点为B,过F,B,C三点作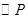 ,其中圆心P的坐标为
,其中圆心P的坐标为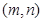 .(1) 若FC是
.(1) 若FC是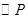 的直径,求椭圆的离心率;(2)若
的直径,求椭圆的离心率;(2)若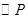 的圆心在直线
的圆心在直线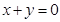 上,求椭圆的方程.
上,求椭圆的方程.
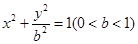 的左焦点为F,左右顶点分别为A,C上顶点为B,过F,B,C三点作
的左焦点为F,左右顶点分别为A,C上顶点为B,过F,B,C三点作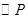 ,其中圆心P的坐标为
,其中圆心P的坐标为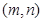 .(1) 若FC是
.(1) 若FC是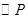 的直径,求椭圆的离心率;(2)若
的直径,求椭圆的离心率;(2)若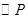 的圆心在直线
的圆心在直线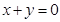 上,求椭圆的方程.
上,求椭圆的方程.(1)椭圆的离心率 ;(2)椭圆的方程为
;(2)椭圆的方程为 。
。
 ;(2)椭圆的方程为
;(2)椭圆的方程为 。
。(1)由椭圆的方程知a=1,再根据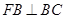 ,转化为
,转化为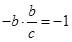 ,再结合
,再结合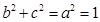 ,从而可得c,进而得到e.
,从而可得c,进而得到e.
(II) 圆心P既在FC的垂直平分线上,也在BC的垂直平分线上,所以通过解FC的垂直平分线和BC的垂直平分线方程组成的方程组得到圆心P的坐标,再根据P点在直线m+n=0上,从而可建立关于b,c的方程.根据a=1,解出b,c的值,求出椭圆方程.
解:(1)由椭圆的方程知 ,∴点
,∴点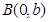 ,
,
 ,
,
设 的坐标为
的坐标为 ,………………1分
,………………1分
∵FC是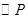 的直径,
的直径,
∴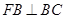
∵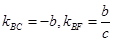 ∴
∴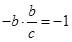 --------------------2分
--------------------2分
∴ ,
, ----------------------------------------3分
----------------------------------------3分
解得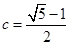 --------------------------------------5分
--------------------------------------5分
∴ 椭圆的离心率
椭圆的离心率 --------------------6分
--------------------6分
(2)∵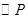 过点F,B,C三点,
过点F,B,C三点,
∴圆心P既在FC的垂直平分线上,也在BC的垂直平分线上,
FC的垂直平分线方程为 --------①
--------①
-----------7分
∵BC的中点为 ,
,
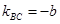
∴BC的垂直平分线方程为 -----②
-----②
---------9分
由①②得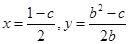 ,
,
即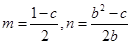 -----11分
-----11分
∵P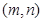 在直线
在直线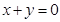 上,∴
上,∴ 

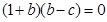
∵ ∴
∴ -----------------13分
-----------------13分
由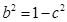 得
得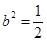
∴椭圆的方程为 ---------------------14分
---------------------14分
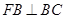 ,转化为
,转化为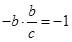 ,再结合
,再结合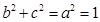 ,从而可得c,进而得到e.
,从而可得c,进而得到e.(II) 圆心P既在FC的垂直平分线上,也在BC的垂直平分线上,所以通过解FC的垂直平分线和BC的垂直平分线方程组成的方程组得到圆心P的坐标,再根据P点在直线m+n=0上,从而可建立关于b,c的方程.根据a=1,解出b,c的值,求出椭圆方程.
解:(1)由椭圆的方程知
 ,∴点
,∴点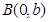 ,
,
 ,
,设
 的坐标为
的坐标为 ,………………1分
,………………1分∵FC是
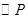 的直径,
的直径,∴
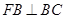
∵
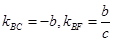 ∴
∴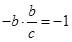 --------------------2分
--------------------2分∴
 ,
, ----------------------------------------3分
----------------------------------------3分解得
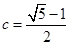 --------------------------------------5分
--------------------------------------5分∴
 椭圆的离心率
椭圆的离心率 --------------------6分
--------------------6分(2)∵
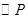 过点F,B,C三点,
过点F,B,C三点,∴圆心P既在FC的垂直平分线上,也在BC的垂直平分线上,
FC的垂直平分线方程为
 --------①
--------① -----------7分
∵BC的中点为
 ,
,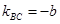
∴BC的垂直平分线方程为
 -----②
-----②---------9分
由①②得
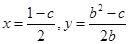 ,
,即
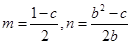 -----11分
-----11分∵P
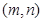 在直线
在直线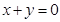 上,∴
上,∴ 

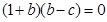
∵
 ∴
∴ -----------------13分
-----------------13分由
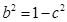 得
得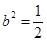
∴椭圆的方程为
 ---------------------14分
---------------------14分
练习册系列答案
相关题目
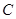 :
: 的左、右顶点分别为
的左、右顶点分别为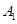 ,
, ,
, 为短轴的端点,△
为短轴的端点,△ 的面积为
的面积为 ,离心率是
,离心率是 .
. 是椭圆
是椭圆 ,
, 与直线
与直线 分别交于
分别交于 ,
, 两点,证明:以
两点,证明:以 为直径的圆与直线
为直径的圆与直线 相切于点
相切于点 (
(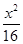 +
+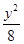 =1的离心率为( )
=1的离心率为( )


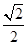
 的离心率为
的离心率为 ,直线
,直线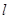 :
: 与以原点为圆心、以椭圆
与以原点为圆心、以椭圆 的短半轴长为半径的圆相切.
的短半轴长为半径的圆相切. ,右焦点
,右焦点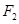 ,直线
,直线 过点
过点 垂
垂 ,线段
,线段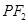 垂直平分线交
垂直平分线交 ,求点
,求点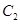 的方程;
的方程;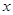 轴上时,在曲线
轴上时,在曲线 在横坐标为
在横坐标为 的点处的切线为L,则点(3,2)到L的距离是
的点处的切线为L,则点(3,2)到L的距离是



 的距离之和等于4,设点P的轨迹为C。
的距离之和等于4,设点P的轨迹为C。 与C交于A、B两点,k为何值时
与C交于A、B两点,k为何值时 ?
? 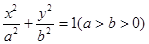 上有一动点P,P到椭圆C的两焦点 F1,F2的距离之和等于2
上有一动点P,P到椭圆C的两焦点 F1,F2的距离之和等于2 ,△PF1F2的面积最大值为1
,△PF1F2的面积最大值为1 (O为坐标原点)且
(O为坐标原点)且 | ,求实数t的取值范围.
| ,求实数t的取值范围.  ,
,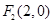 ,曲线
,曲线 上的动点
上的动点 满足
满足 ,直线
,直线 与曲线
与曲线 .
. ,若
,若
 ,求直线
,求直线 的方程.
的方程. 上一点,F1、F2是椭圆的两个焦点,
上一点,F1、F2是椭圆的两个焦点, ,则△F1PF2的面积是 .
,则△F1PF2的面积是 .