题目内容
若函数f（x）=|x2-4x|-a有三个零点，则实数a的值是 ．
考点：函数零点的判定定理
专题：常规题型,函数的性质及应用
分析：将函数零点化为方程解的个数讨论．
解答：
解：若函数f（x）=|x2-4x|-a有三个零点，
则方程|x2-4x|-a=0有三个不同的根，
即方程|x2-4x|=a有三个不同的根，
则可知a＞0，
则原方程可化为：x2-4x-a=0或x2-4x+a=0；
∵x2-4x-a=0一定有两个不同的根，
则方程x2-4x+a=0有两个相同的根；
则a=4．
经验证，此时函数f（x）=|x2-4x|-a有三个零点．
故答案为4．
则方程|x2-4x|-a=0有三个不同的根，
即方程|x2-4x|=a有三个不同的根，
则可知a＞0，
则原方程可化为：x2-4x-a=0或x2-4x+a=0；
∵x2-4x-a=0一定有两个不同的根，
则方程x2-4x+a=0有两个相同的根；
则a=4．
经验证，此时函数f（x）=|x2-4x|-a有三个零点．
故答案为4．
点评：本题考查了函数零点与相应方程的解的关系，属于基础题．
练习册系列答案
相关题目
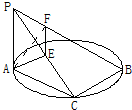如图PA⊥⊙O所在平面，AB是⊙O的直径，C是⊙O上一点，E、F分别是点A在PC、PB上的射影，给出下列结论：设集合M={0，1，2}，N={x|x2≤x}，则M∩N=（ ）
| A、{0} | B、{1} |
| C、{0，1} | D、{0，1，2} |