题目内容
3. 如图,在三棱锥P-ABC中,AB⊥BC,PA=PB,E为AC的中点
如图,在三棱锥P-ABC中,AB⊥BC,PA=PB,E为AC的中点(1)求证:PE⊥AB
(2)设平面PAB⊥平面ABC,PB=BC=2,AC=4,求二面角B-PA-C的平面角的正弦值.
分析 (1)连接PD,由等腰三角形三线合一,可得PD⊥AB,由DE∥BC,BC⊥AB可得DE⊥AB,进而由线面垂直的判定定理得到AB⊥平面PDE,再由线面垂直的性质得到AB⊥PE;
(2)以D为原点建立空间直角坐标系,分别求出平面PAE的法向量和平面PAB的法向量,代入向量夹角公式,可得二面角B-PA-C的平面角的正弦值.
解答 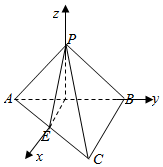 (1)证明:取AB的中点D,连接PD,
(1)证明:取AB的中点D,连接PD,
∵PA=PB,D为AB中点,
∴PD⊥AB.
∵D、E分别为AB、AC中点,
∴DE∥BC,
∵BC⊥AB,
∴DE⊥AB,
又∵PD∩DE=D,PD,DE?平面PDE
∴AB⊥平面PDE,
∵PE?平面PDE,
∴PE⊥AB;
(2)解:∵平面PAB⊥平面ABC,ED⊥AB,
∴ED⊥平面PAB,则PD⊥DE.
如图,以D为原点建立空间直角坐标系,由PA=PB=BC=2,AC=4,
则A(0,-$\sqrt{3}$,0),P(0,0,1),E(1,0,0),
∴$\overrightarrow{AP}$=(0,$\sqrt{3}$,1),$\overrightarrow{AE}$=(1,$\sqrt{3}$,0).
设平面PAC的法向量$\overrightarrow{m}$=(x,y,z),
则$\left\{\begin{array}{l}{\overrightarrow{m}•\overrightarrow{AP}=\sqrt{3}y+z=0}\\{\overrightarrow{m}•\overrightarrow{AE}=x+\sqrt{3}y=0}\end{array}\right.$,令z=$\sqrt{3}$,得$\overrightarrow{m}$=($\sqrt{3}$,-1,$\sqrt{3}$)
∵DE⊥平面PAB,
∴平面PAB的法向量为$\overrightarrow{n}$=(1,0,0),
∴cos<$\overrightarrow{m},\overrightarrow{n}$>=$\frac{\overrightarrow{m}•\overrightarrow{n}}{|\overrightarrow{m}||\overrightarrow{n}|}=\frac{\sqrt{3}}{\sqrt{7}×1}=\frac{\sqrt{21}}{7}$.
∴二面角B-PA-C的平面角的正弦值为$\frac{\sqrt{21}}{7}$.
点评 本题考查线面垂直的判定和性质,考查空间想象能力和思维能力,训练了利用空间向量求解二面角的平面角,是中档题.

 启东小题作业本系列答案
启东小题作业本系列答案 如图,网格纸上小正方形的边长为1,粗线画出的是某几何体的三视图,已知该几何体的各个面中有n个面是矩形,体积为V,则( )
如图,网格纸上小正方形的边长为1,粗线画出的是某几何体的三视图,已知该几何体的各个面中有n个面是矩形,体积为V,则( )| A. | n=4,V=10 | B. | n=5,V=12 | C. | n=4,V=12 | D. | n=5,V=10 |
| 患心肺疾病 | 不患心肺疾病 | 合计 | |
| 男 | 20 | 5 | 25 |
| 女 | 10 | 15 | 25 |
| 合计 | 30 | 20 | 50 |
(2)已知在患心肺疾病的10位女性中,有3位又患有胃病,现在从患心肺疾病的10位女性中,选出3位进行其他方面的排查,其中患胃病的人数为ξ,求ξ的分布列、数学期望
参考公式:K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$,其中n=a+b+c+d
下面的临界值表仅供参考.
| P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
| A. | $\frac{7}{8}$ | B. | $\frac{5}{8}$ | C. | $\frac{1}{2}$ | D. | $\frac{3}{8}$ |
