如图.网格纸上小正方形的边长为1.粗线画出的是某几何体的三视图.已知该几何体的各个面中有n个面是矩形.体积为V.则( )A．n=4.V=10B．n=5.V=12C．n=4.V=12D．n=5.V=10 题目和参考答案——青夏教育精英家教网——

题目内容

9．

如图，网格纸上小正方形的边长为1，粗线画出的是某几何体的三视图，已知该几何体的各个面中有n个面是矩形，体积为V，则（　　）

A．

n=4，V=10

B．

n=5，V=12

C．

n=4，V=12

D．

n=5，V=10

分析由三视图还原原几何体，可知该几何体为直五棱柱，然后由棱柱体积公式求解．

解答解：由三视图可知，该几何体为直五棱柱，
如图：
故n=5，且V=$2×（{2}^{2}+\frac{1}{2}×2×1）=10$．
故选：D．

点评本题考查由三视图求几何体的体积，关键是由三视图还原原几何体，是中档题．

练习册系列答案

单元评估AB卷系列答案

非常学案系列答案

四项专练系列答案

备战中考信息卷系列答案

活力英语全程检测卷系列答案

浙江专版课时导学案系列答案

龙江王中王中考总复习系列答案

名师优选卷系列答案

青海省中考模拟试卷系列答案

中考指导系列答案

相关题目

19．有甲、乙、丙、丁四位歌手参加比赛，其中只有一位获奖，有人走访了四位歌手，甲说：“是乙或丙获奖”；乙说：“甲、丙都未获奖”；丙说：“我获奖了”，丁说：“是乙获奖”．若四位歌手的话只有一句是错的，则获奖的歌手是（　　）

20．若函数f（x）的导数f′（x）存在导数，记f′（x）的导数为fⁿ（x）．如果f（x）对任意x∈（a，b），都有fⁿ（x）＜0成立，则f（x）有如下性质：
f（$\frac{{x}_{1}+{x}_{2}+…+{x}_{n}}{n}$）≥$\frac{f（{x}_{1}）+f（{x}_{2}）+…+f（{x}_{n}）}{n}$．其中n∈N^*，x₁，x₂，…，x_n∈（a，b）．若f（x）=sinx，则fⁿ（x）=-sinx；根据上述性质推断：当x₁+x₂+x₃=π且x₁，x₂，x₃∈（0，π）时，根据上述性质推断：sinx₁+sinx₂+sinx₃的最大值为$\frac{2\sqrt{3}}{3}$．

17．已知函数f（x）=Asin（ωx+φ），其中A＞0，ω＞0，0＜φ＜π，且函数f（x）的最小正周期为$\frac{π}{2}$．
（1）若函数f（x）在x=$\frac{π}{3}$处取到最小值-2，求函数f（x）的解析式；
（2）若将函数f（x）图象上所有点的横坐标伸长到原来的2倍（纵坐标不变），再将向左平移$\frac{π}{6}$个单位，得到的函数图象关于y轴对称，求函数f（x）的单调递增区间．

4．若集合A={0，1，2}，B={x|x²≤4，x∈N}，则A∩B=（　　）

14．在极坐标系中，曲线C的极坐标方程为ρ=2cosθ+2sinθ（0≤θ＜2π），点M（1，$\frac{π}{2}$），以极点O为原点，以极轴为x轴的正半轴建立平面直角坐标系．已知直线l：$\left\{\begin{array}{l}{x=\frac{\sqrt{2}}{2}t}\\{y=1+\frac{\sqrt{2}}{2}t}\end{array}\right.$（t为参数）与曲线C交于A，B两点，且|MA|＞|MB|．
（1）若P（ρ，θ）为曲线C上任意一点，求ρ的最大值，并求此时点P的极坐标；
（2）求$\frac{|MA|}{|MB|}$．

6．函数f（x）=sin²x+$\sqrt{3}$sinxcosx+1图象的一条对称轴方程为（　　）

x=$\frac{π}{2}$

x=$\frac{π}{3}$

x=$\frac{π}{4}$

x=$\frac{π}{6}$

如图，在三棱锥P-ABC中，AB⊥BC，PA=PB，E为AC的中点
（1）求证：PE⊥AB
（2）设平面PAB⊥平面ABC，PB=BC=2，AC=4，求二面角B-PA-C的平面角的正弦值．

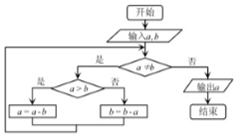如图所示程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”，执行该程序框图，若输入a，b分别为8，18，则输出的a等于（　　）