题目内容

12．现有八个数，它们能构成一个以1为首项．-3为公比的等比数列，若从这八个数中随机抽取一个数，则它大于8的概率是（　　）
A．$\frac{7}{8}$B．$\frac{5}{8}$C．$\frac{1}{2}$D．$\frac{3}{8}$

分析 先由题意写出成等比数列的8个数，然后找出大于8的项的个数，代入古典概论的计算公式即可求解．

解答 解：由题意成等比数列的8个数为：1，-3，（-3）2，（-3）3…（-3）7；
其中大于8的项有：（-3）2，（-3）4，（-3）6，共3个数
这8个数中随机抽取一个数，则它大于8的概率是P=$\frac{3}{8}$；
故选D．

点评 本题主要考查了等比数列的通项公式及古典概率的计算公式的应用，属于基础试题．

练习册系列答案
相关题目
17．已知函数f（x）=Asin（ωx+φ），其中A＞0，ω＞0，0＜φ＜π，且函数f（x）的最小正周期为$\frac{π}{2}$．
（1）若函数f（x）在x=$\frac{π}{3}$处取到最小值-2，求函数f（x）的解析式；
（2）若将函数f（x）图象上所有点的横坐标伸长到原来的2倍（纵坐标不变），再将向左平移$\frac{π}{6}$个单位，得到的函数图象关于y轴对称，求函数f（x）的单调递增区间．
3．如图，在三棱锥P-ABC中，AB⊥BC，PA=PB，E为AC的中点
（1）求证：PE⊥AB
（2）设平面PAB⊥平面ABC，PB=BC=2，AC=4，求二面角B-PA-C的平面角的正弦值．
20．cos3tan4的值（　　）
A．小于0B．大于0C．等于0D．不存在
7．已知f（x）=$\left\{\begin{array}{l}{\sqrt{x}（0≤x≤1）}\\{\sqrt{2x-{x}^{2}}（1＜x≤2）}\end{array}\right.$．
（1）求f（x）的最大值；
（2）求f（x）与x轴围成的面积．
17．已知函数f（x）=lnx-$\frac{1}{2}$ax2+bx+1的图象在x=1处的切线l过点（$\frac{1}{2}$，$\frac{1}{2}$）．
（1）若函数g（x）=f（x）-（a-1）x（a＞0），求g（x）最大值（用a表示）；
（2）若a=-4，f（x1）+f（x2）+x1+x2+3x1x2=2，证明：x1+x2≥$\frac{1}{2}$．
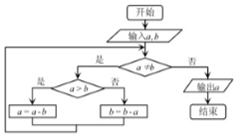4．如图所示程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”，执行该程序框图，若输入a，b分别为8，18，则输出的a等于（　　）
A．2B．4C．6D．8
1．如图所示，正方体ABCD-A′B′C′D′的棱长为1，E、F分别是棱AA′，CC′的中点，过直线EF的平面分别与棱BB′，DD′交于M，N，给出以下四个命题：
①平面MENF一定为矩形；
②平面MENF⊥平面BDD′B′；
③当M为BB1的中点时，MENF的面积最小；
④四棱锥A-MENF的体积为常数．
以上命题中正确命题的序号为②③④．
12．二阶矩阵M对应的变换T将点（-2，1）与（1，0）分别变换成点（3，0）与（1，2）．求矩阵M的特征值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网