题目内容
（2012•绵阳三模）已知双曲线C：
-
=1（a＞0，b＞0）的右焦点为F，过F且斜率为
的直线交C于A，B两点，若
=5
，则C的离心率为（ ）
| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
| AF |
| FB |
分析：设出|BF|=x，|AF|=5x，利用双曲线的第二定义，结合斜率为
，建立等式，即可求得双曲线的离心率．
| 3 |
解答：解：由题意，设|BF|=x，则|AF|=5x
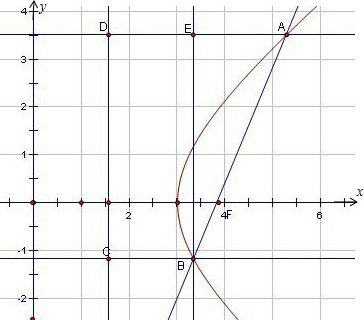
根据双曲线的第二定义可得|AD|=
，|BC|=
∴|AE|=
由斜率为
，可得|AB|=2|AE|
∴|AB|=|AF|+|BF|=6x=2AE=2×
∴e=
故选A．
根据双曲线的第二定义可得|AD|=
| 5x |
| e |
| x |
| e |
∴|AE|=
| 4x |
| e |
由斜率为
| 3 |
∴|AB|=|AF|+|BF|=6x=2AE=2×
| 4x |
| e |
∴e=
| 4 |
| 3 |
故选A．
点评：本题考查双曲线的离心率，考查学生分析解决问题的能力，属于中档题．
练习册系列答案
相关题目
（2012•绵阳三模）已知函数f（x）=Asin（wx+φ）（A＞0，w＞0，|φ|＜