题目内容
已知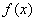 是定义在R上的偶函数,且
是定义在R上的偶函数,且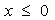 时,
时,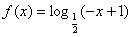 .
.
(Ⅰ)求函数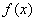 的解析式;
的解析式;
(Ⅱ)若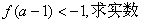
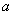 的取值范围.
的取值范围.
解:(Ⅰ)令x>0,则-x<0,
从而f(-x)=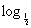 (x+1)=f(x),
(x+1)=f(x),
∴x>0时,f(x)=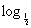 (x+1).
(x+1).
∴函数f(x)的解析式为f(x)=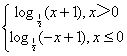 .
.
(Ⅱ)设x1, x2是任意两个值,且x1<x2≤0,
则-x1>-x2≥0,∴1-x1>1-x2.
∵f(x2)-f(x1)
=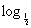 (-x2+1)-
(-x2+1)-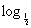 (-x1+1)
(-x1+1)
=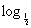
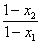 >
>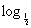 1=0,∴f(x2)>f(x1),
1=0,∴f(x2)>f(x1),
∴f(x)=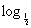 (-x+1)在(-∞, 0]上为增函数. 又f(x)是定义在R上的偶函数,
(-x+1)在(-∞, 0]上为增函数. 又f(x)是定义在R上的偶函数,
∴f(x)在(0, +∞)上为减函数.
∵f(a-1)<-1=f(1),∴|a-1|>1,解得a>2或a<0.
故实数a的取值范围为(-∞, 0)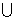 (2, +∞).
(2, +∞).

练习册系列答案
相关题目
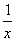 (x>0)的图象上.若点Bn的坐标为(n,0)(n≥2,n∈N*),记矩形AnBnCnDn的周长为an,则a2+a3+…+a10=( )
(x>0)的图象上.若点Bn的坐标为(n,0)(n≥2,n∈N*),记矩形AnBnCnDn的周长为an,则a2+a3+…+a10=( )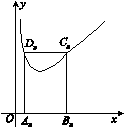
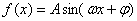 (其中A>0,
(其中A>0,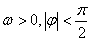 )的图像如图所示,为了得到
)的图像如图所示,为了得到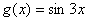 的图像,则只要将
的图像,则只要将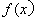 的图像( )
的图像( )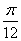 个单位长度
个单位长度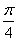 个单位长度
个单位长度 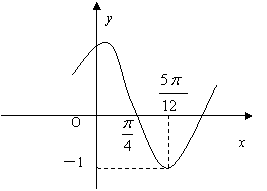
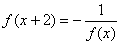 ,当
,当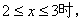
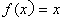 ,则
,则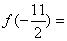
 __________.
__________. 、m、n是互不相同的空间直线,α、β是不重合的平面,则下列命题中为真命题的是( )
、m、n是互不相同的空间直线,α、β是不重合的平面,则下列命题中为真命题的是( )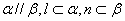 ,则
,则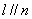 B.若
B.若 ,则
,则
 ,则
,则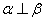 D.若
D.若 ,则
,则
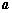 与
与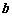 的夹角为
的夹角为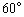 ,
, ,
,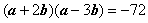 ,则
,则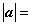 ( )
( )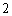 B.4 C.6 D.12
B.4 C.6 D.12 的椭圆C:
的椭圆C: 和双曲线
和双曲线 的离心率互为倒
的离心率互为倒 ,且
,且 与椭圆的公共
与椭圆的公共