题目内容
16.函数$y={log_{\frac{1}{3}}}({{x^2}-6x+5})$的单调递减区间为(5,+∞).分析 由对数式的真数大于0求出函数的定义域,再求出内函数二次函数的增区间,结合复合函数的单调性可得原函数的减区间.
解答 解:由x2-6x+5>0,解得x<1或x>5.
内函数t=x2-6x+5在(5,+∞)上为增函数,
而外函数y=$lo{g}_{\frac{1}{3}}t$为减函数,
∴复合函数$y={log_{\frac{1}{3}}}({{x^2}-6x+5})$的单调递减区间为(5,+∞).
故答案为:(5,+∞).
点评 本题主要考查了复合函数的单调性以及单调区间的求法.对应复合函数的单调性,一要注意先确定函数的定义域,二要利用复合函数与内层函数和外层函数单调性之间的关系进行判断,判断的依据是“同增异减”,是中档题.

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
5.已知不等式组$\left\{\begin{array}{l}x+y+2≤0\\ x-y+4≥0\\ y≥a\end{array}\right.$,若z=2x-y的最大值为-1,则a值为( )
| A. | -1 | B. | 0 | C. | 1 | D. | 2 |
6.经过抛物线$y=\frac{1}{4}x^2$的焦点与圆 x2-4x+y2=0相切的直线方程为( )
| A. | 225x-64y+4=0或x=0 | B. | 3x-4y+4=0 | ||
| C. | x=0 | D. | 3x-4y+4=0或x=0 |
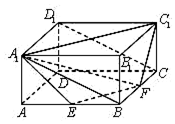 如图,在长方体ABCD-A1B1C1D1中,AA1=1,AB=AD=2,E,F分别是棱AB,BC的中点,证明A1,C1,F,E四点共面,并求点B到平面A1EF的距离.
如图,在长方体ABCD-A1B1C1D1中,AA1=1,AB=AD=2,E,F分别是棱AB,BC的中点,证明A1,C1,F,E四点共面,并求点B到平面A1EF的距离.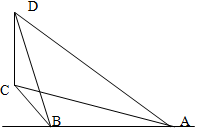 一辆汽车在一条水平的公路上向正西行驶,到A处时测得公路北侧远处一山顶D在西偏北15.的方向上,行驶5km后到达B处,测得此山顶在西偏北45.的方向上,此时看山顶的仰角为30,求此山CD的高.
一辆汽车在一条水平的公路上向正西行驶,到A处时测得公路北侧远处一山顶D在西偏北15.的方向上,行驶5km后到达B处,测得此山顶在西偏北45.的方向上,此时看山顶的仰角为30,求此山CD的高.