题目内容
4.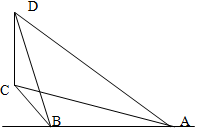 一辆汽车在一条水平的公路上向正西行驶,到A处时测得公路北侧远处一山顶D在西偏北15.的方向上,行驶5km后到达B处,测得此山顶在西偏北45.的方向上,此时看山顶的仰角为30,求此山CD的高.
一辆汽车在一条水平的公路上向正西行驶,到A处时测得公路北侧远处一山顶D在西偏北15.的方向上,行驶5km后到达B处,测得此山顶在西偏北45.的方向上,此时看山顶的仰角为30,求此山CD的高.
分析 在△ABC中,利用正弦定理计算BC,再在Rt△BCD中求出CD.
解答 解:由题意可知AB=5,∠CAB=15°,∠ABC=135°,∠DBC=30°,
∴∠ACB=30°,
在△ABC中,由正弦定理得:$\frac{AB}{sin∠ACB}=\frac{BC}{sin∠BAC}$,
∴BC=$\frac{AB•sin∠CAB}{sin∠ACB}$=$\frac{5sin15°}{sin30°}$=10sin15°=$\frac{5(\sqrt{6}-\sqrt{2})}{2}$,
在Rt△BCD中,∵$\frac{CD}{BC}$=tan∠DBC=$\frac{\sqrt{3}}{3}$,
∴CD=$\frac{\sqrt{3}}{3}$BC=$\frac{\sqrt{3}}{3}×$$\frac{5(\sqrt{6}-\sqrt{2})}{2}$=$\frac{5\sqrt{2}}{2}$-$\frac{5\sqrt{6}}{6}$.
点评 本题考查了正弦定理,解三角形的实际应用,属于基础题.

练习册系列答案
 优加精卷系列答案
优加精卷系列答案
相关题目
14.设全集为U,若A∩∁UB={1},A∩B={2},则集合A可表示为( )
| A. | {1} | B. | {1,2} | C. | {2} | D. | ∅ |
15.为了探究电离辐射的剂量与人体的受损程度是否有关,用两种不同剂量的电离辐射照射小白鼠.在照射14天内的结果如表所示:
进行统计分析时的统计假设是小白鼠的死亡与剂量无关.
解析 根据独立性检验的基本思想,可知类似于反证法,即要确认“两个分量有关系”这一结论成立的可信程度,首先假设该结论不成立.对于本题,进行统计分析时的统计假设应为“小白鼠的死亡与剂量无关”.
| 死亡 | 存活 | 总计 | |
| 第一种剂量 | 14 | 11 | 25 |
| 第二种剂量 | 6 | 19 | 25 |
| 总计 | 20 | 30 | 50 |
解析 根据独立性检验的基本思想,可知类似于反证法,即要确认“两个分量有关系”这一结论成立的可信程度,首先假设该结论不成立.对于本题,进行统计分析时的统计假设应为“小白鼠的死亡与剂量无关”.
13. 已知函数f(x)的定义域[-1,5],部分对应值如表,f(x)的导函数f′(x),的图象如图所示,
已知函数f(x)的定义域[-1,5],部分对应值如表,f(x)的导函数f′(x),的图象如图所示,
下列关于函数f(x)的命题:
①函数f(x)的值域为[1,4];
②函数f(x)在[0,2]上是减函数;
③如果当x∈[-1,t]时,f(x)的最大值是4,那么t的最大值为4;
④当1<a<4时,函数y=f(x)-a最多有4个零点.
其中正确的命题个数为( )
 已知函数f(x)的定义域[-1,5],部分对应值如表,f(x)的导函数f′(x),的图象如图所示,
已知函数f(x)的定义域[-1,5],部分对应值如表,f(x)的导函数f′(x),的图象如图所示,| x | -1 | 0 | 2 | 4 | 5 |
| f(x) | 1 | 4 | 1.5 | 4 | 1 |
①函数f(x)的值域为[1,4];
②函数f(x)在[0,2]上是减函数;
③如果当x∈[-1,t]时,f(x)的最大值是4,那么t的最大值为4;
④当1<a<4时,函数y=f(x)-a最多有4个零点.
其中正确的命题个数为( )
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
14.若复数z=1+2i,则复数z的模等于( )
| A. | $\sqrt{5}$ | B. | 2 | C. | $\sqrt{3}$ | D. | $\sqrt{2}$ |