题目内容
如图甲,在直角梯形 中,
中, ,
, ,
, ,
, 是
是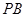 的中点. 现沿
的中点. 现沿 把平面
把平面 折起,使得
折起,使得 (如图乙所示),
(如图乙所示),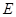 、
、 分别为
分别为 、
、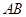 边的中点.
边的中点.
(Ⅰ)求证: 平面
平面 ;
;
(Ⅱ)求证:平面 平面
平面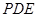 ;
;
(Ⅲ)在 上找一点
上找一点 ,使得
,使得 平面
平面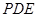 .
.

 中,
中, ,
, ,
, ,
, 是
是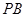 的中点. 现沿
的中点. 现沿 把平面
把平面 折起,使得
折起,使得 (如图乙所示),
(如图乙所示),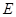 、
、 分别为
分别为 、
、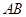 边的中点.
边的中点.(Ⅰ)求证:
 平面
平面 ;
; (Ⅱ)求证:平面
 平面
平面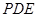 ;
;(Ⅲ)在
 上找一点
上找一点 ,使得
,使得 平面
平面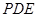 .
. 
(Ⅰ)证:因为PA⊥AD,PA⊥AB,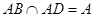 ,所以
,所以 平面
平面 …4分
…4分
(Ⅱ)证:因为 ,A是PB的中点,所以ABCD是矩形,又E为BC边的中点,所以AE⊥ED。又由
,A是PB的中点,所以ABCD是矩形,又E为BC边的中点,所以AE⊥ED。又由 平面
平面 ,得
,得
 ,且
,且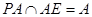 ,所以
,所以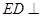 平面
平面 ,而
,而 平面
平面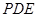 ,
,
故平面 平面
平面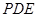 ……………………………………………9分
……………………………………………9分
(Ⅲ)过点 作
作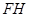 ∥
∥ 交
交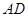 于
于 ,再过
,再过 作
作 ∥
∥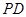 交
交 于
于 ,连结
,连结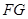 。
。
由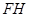 ∥
∥ ,
, 平面
平面 ,得
,得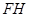 ∥平面
∥平面 ;
;
由 ∥
∥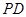 ,
, 平面
平面 ,得
,得 ∥平面
∥平面 ,
,
又 ,所以平面
,所以平面 ∥平面
∥平面 …………………………12分
…………………………12分
再分别取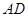 、
、 的中点
的中点 、
、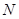 ,连结
,连结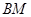 、
、 ,易知
,易知 是
是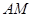 的中点,
的中点, 是
是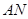 的中点,
的中点,
从而当点 满足
满足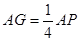 时,有
时,有 平面
平面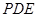 。
。
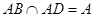 ,所以
,所以 平面
平面 …4分
…4分(Ⅱ)证:因为
 ,A是PB的中点,所以ABCD是矩形,又E为BC边的中点,所以AE⊥ED。又由
,A是PB的中点,所以ABCD是矩形,又E为BC边的中点,所以AE⊥ED。又由 平面
平面 ,得
,得
 ,且
,且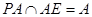 ,所以
,所以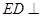 平面
平面 ,而
,而 平面
平面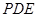 ,
,故平面
 平面
平面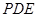 ……………………………………………9分
……………………………………………9分(Ⅲ)过点
 作
作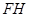 ∥
∥ 交
交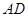 于
于 ,再过
,再过 作
作 ∥
∥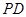 交
交 于
于 ,连结
,连结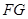 。
。由
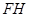 ∥
∥ ,
, 平面
平面 ,得
,得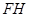 ∥平面
∥平面 ;
;由
 ∥
∥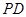 ,
, 平面
平面 ,得
,得 ∥平面
∥平面 ,
,又
 ,所以平面
,所以平面 ∥平面
∥平面 …………………………12分
…………………………12分再分别取
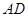 、
、 的中点
的中点 、
、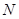 ,连结
,连结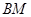 、
、 ,易知
,易知 是
是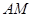 的中点,
的中点, 是
是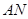 的中点,
的中点,从而当点
 满足
满足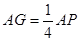 时,有
时,有 平面
平面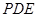 。
。略

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

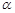 的一个充分条件是( )
的一个充分条件是( )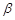 ,
,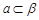 ,
,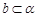 ,a∥b
,a∥b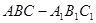 中,
中,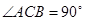 ,
,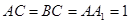 ,
,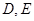 分别为棱
分别为棱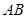 、
、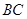 的中点,
的中点,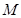 为棱
为棱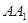 上的点。
上的点。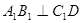 ;
;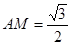 时,求二面角
时,求二面角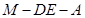 的大小。
的大小。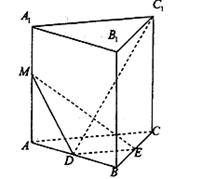
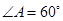 、边长为
、边长为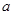 的菱形,又
的菱形,又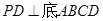 ,且PD=CD,点M、N分别是棱AD、PC的中点.
,且PD=CD,点M、N分别是棱AD、PC的中点.
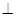 平面PAD;
平面PAD;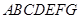 中,平面
中,平面 ∥平面
∥平面 ,
, 平面
平面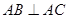 ,
, ,
,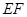 ∥
∥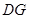 ,且
,且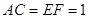 ,
,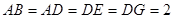 .
.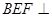 平面
平面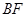 ∥平面
∥平面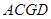 ;
;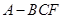 的体积.
的体积.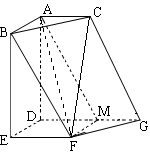

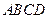 中,
中, 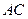 平行于截面
平行于截面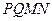
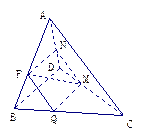
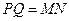 ,证明
,证明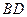 ∥平面
∥平面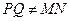 ,猜想三条直线
,猜想三条直线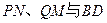 位置关系,并证明之.
位置关系,并证明之.
