题目内容
(本小题14分)已知四棱锥P-ABCD,底面ABCD是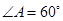 、边长为
、边长为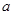 的菱形,又
的菱形,又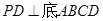 ,且PD=CD,点M、N分别是棱AD、PC的中点.
,且PD=CD,点M、N分别是棱AD、PC的中点.

(1)证明:DN//平面PMB;
(2)证明:平面PMB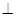 平面PAD;
平面PAD;
(3)求点A到平面PMB的距离.
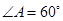 、边长为
、边长为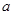 的菱形,又
的菱形,又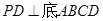 ,且PD=CD,点M、N分别是棱AD、PC的中点.
,且PD=CD,点M、N分别是棱AD、PC的中点.
(1)证明:DN//平面PMB;
(2)证明:平面PMB
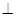 平面PAD;
平面PAD;(3)求点A到平面PMB的距离.
解:(1)证明:取PB中点Q,连结MQ、NQ,
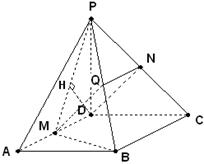
因为M、N分别是棱AD、PC中点,所以
QN//BC//MD,且QN=MD,于是DN//MQ.
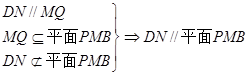 .… …………………6分
.… …………………6分
(2)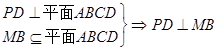
又因为底面ABCD是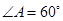 、边长为
、边长为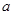 的菱形,且M为AD中点,
的菱形,且M为AD中点,
所以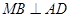 .又
.又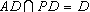 所以
所以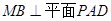 .
.
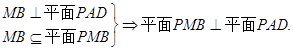 ………………10分
………………10分
(3)因为M是AD中点,所以点A与D到平面PMB等距离.
过点D作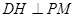 于H,由(2)平面PMB
于H,由(2)平面PMB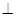 平面PAD,所以
平面PAD,所以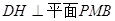 .
.
故DH是点D到平面PMB的距离.
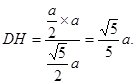 所以点A到平面PMB的距离为
所以点A到平面PMB的距离为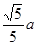 .………14分
.………14分

因为M、N分别是棱AD、PC中点,所以
QN//BC//MD,且QN=MD,于是DN//MQ.
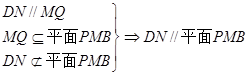 .… …………………6分
.… …………………6分(2)
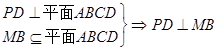
又因为底面ABCD是
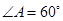 、边长为
、边长为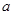 的菱形,且M为AD中点,
的菱形,且M为AD中点,所以
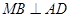 .又
.又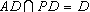 所以
所以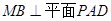 .
. ………………10分
………………10分(3)因为M是AD中点,所以点A与D到平面PMB等距离.
过点D作
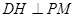 于H,由(2)平面PMB
于H,由(2)平面PMB 平面PAD,所以
平面PAD,所以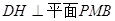 .
.故DH是点D到平面PMB的距离.
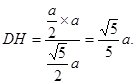 所以点A到平面PMB的距离为
所以点A到平面PMB的距离为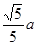 .………14分
.………14分略

练习册系列答案
相关题目
 , 点P为矩形ABCD所
, 点P为矩形ABCD所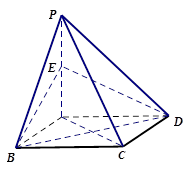
 、
、 .有下列命题
.有下列命题


 平行于平面
平行于平面 内的无数条直线,则下列结论正确的是
内的无数条直线,则下列结论正确的是


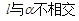
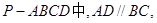
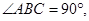
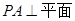
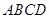 ,
,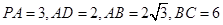 ,
, 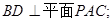
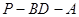 的大小.
的大小.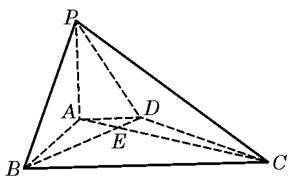
 中,
中, ,
, ,
, ,
, 是
是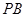 的中点. 现沿
的中点. 现沿 把平面
把平面 折起,使得
折起,使得 (如图乙所示),
(如图乙所示),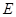 、
、 分别为
分别为 、
、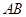 边的中点.
边的中点. 平面
平面 ;
;  平面
平面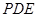 ;
; 上找一点
上找一点 ,使得
,使得 平面
平面
 //平面
//平面 ,平面
,平面 ,则直线
,则直线 的位置关系为 .
的位置关系为 .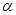 ,a∥平面
,a∥平面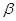 ,
,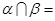 直线b,则( )
直线b,则( )