Question

 已知函数f (x)是正比例函数,函数g(x)是反比例函数,且f(1)=1,g(1)=1.

(1) 求函数f(x),g(x)的解析式;

(2) 判断函数h(x)=f(x)+g(x)的奇偶性;

(3) 求证:函数S(x)=xf(x)+g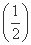在(0,+∞)上是单调增函数.

Answer 1

 (1) 设f(x)=k1x(k1≠0),g(x)=(k2≠0),

因为f(1)=1,g(1)=1,所以k1=1,k2=1.所以f(x)=x,g(x)=.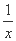

(2) 由(1)得h(x)=x+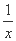,则函数h(x)的定义域是(-∞,0)∪(0,+∞),

h(-x)=-x+=-=-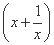h(x),所以函数h(x)=f(x)+g(x)是奇函数.

(3) 由(1)得S(x)=x2+2.设x1,x2∈(0,+∞),且x1<x2,

则S(x1)-S(x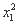2)=(+2)-(+2)=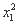-=(x1-x2)(x1+x2).

因为x1,x2∈(0,+∞),且x1<x2,所以x1-x2<0,x1+x2>0,

所以S(x1)-S(x2)<0,所以S(x1)<S(x2).

所以函数S(x)= xf(x)+g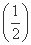在(0,+∞)上是增函数.