题目内容
4．已知等差数列{an}的前n项和为Sn，a1＞0且$\frac{{a}_{6}}{{a}_{5}}$=$\frac{9}{11}$，则Sn为非负值的最大n值为20．分析 设出等差数列的公差d，由$\frac{{a}_{6}}{{a}_{5}}$=$\frac{9}{11}$得到首项和公差的关系，代入等差数列的通项公式，由Sn≥0求出n的范围，再根据n为正整数求得n的值．
解答 解：设等差数列的公差为d，由$\frac{{a}_{6}}{{a}_{5}}$=$\frac{9}{11}$，
得$\frac{{a}_{1}+5d}{{a}_{1}+4d}$=$\frac{9}{11}$，
即2a1+19d=0，解得d=-$\frac{2{a}_{1}}{19}$，
所以Sn=na1+$\frac{n（n-1）}{2}$×（-$\frac{2{a}_{1}}{19}$）≥0，
整理，得：
Sn=na1•$\frac{20-n}{19}$≥0．
因为a1＞0，
所以20-n≥0即n≤20，
故Sn为非负值的最大n值为20．
故答案是：20．
点评 本题考查等差数列的前n项和，考查了不等式的解法，是基础题．
练习册系列答案
相关题目
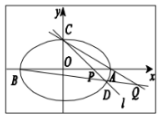过点C（0，$\sqrt{2}$）的椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的离心率为$\frac{\sqrt{2}}{2}$，椭圆与x轴交于两点A（a，0），B（-a，0），过点C的直线l与椭圆交于另一点D，并与x轴交于点P，直线AC与BD交于点Q．