题目内容
(本题满分12分)
已知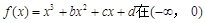 上是增函数,在[0,2]上是减函数,且方程
上是增函数,在[0,2]上是减函数,且方程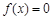 有三个根,它们分别为
有三个根,它们分别为 .
.
(1)求c的值;
(2)求证 ;
;
(3)求 的取值范围.
的取值范围.
已知
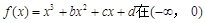 上是增函数,在[0,2]上是减函数,且方程
上是增函数,在[0,2]上是减函数,且方程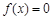 有三个根,它们分别为
有三个根,它们分别为 .
.(1)求c的值;
(2)求证
 ;
;(3)求
 的取值范围.
的取值范围.(1) ;(2)
;(2)
(3)
 ;(2)
;(2)
(3)

本试题主要是考查而来导数在研究函数中的运用。率哟个导数研究函数的极值,以及函数的单调性,进而得到参数的范围,以及不等式的证明。
(1)因为 上是增函数,
上是增函数,
在[0,2]上是减函数,∴当x=0时f(x)取到极大值,
(2) 的两个根分别为
的两个根分别为


(3)利用设根法表示出函数,然后借助于根韦达定理得到根与系数的关系,进而证明不等式。
解:(1) 上是增函数,
上是增函数,
在[0,2]上是减函数,∴当x=0时f(x)取到极大值,
(2) 的两个根分别为
的两个根分别为



(3)




(1)因为
 上是增函数,
上是增函数,在[0,2]上是减函数,∴当x=0时f(x)取到极大值,

(2)
 的两个根分别为
的两个根分别为


(3)利用设根法表示出函数,然后借助于根韦达定理得到根与系数的关系,进而证明不等式。
解:(1)
 上是增函数,
上是增函数,在[0,2]上是减函数,∴当x=0时f(x)取到极大值,

(2)
 的两个根分别为
的两个根分别为



(3)






练习册系列答案
相关题目
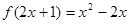 ,则
,则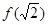 = _________
= _________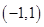 上的函数
上的函数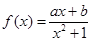 为奇函数,且
为奇函数,且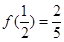
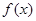 的解析式;
的解析式;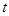 的不等式
的不等式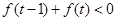 .
.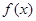 是定义在R上的偶函数,且对任意的
是定义在R上的偶函数,且对任意的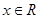 恒有
恒有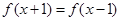 ,
,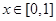 时,
时,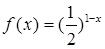 ,则其中所有正确命题的序号是_____________.
,则其中所有正确命题的序号是_____________.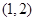 上是减函数,在
上是减函数,在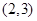 上是增函数;
上是增函数;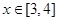 时,
时,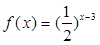 .
. 

 时,求f(x)的单调区间;
时,求f(x)的单调区间; ,若
,若 分别为
分别为 的极大值和极小值,若
的极大值和极小值,若 ,求
,求 取值范围。
取值范围。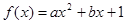 ,
,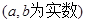 ,
,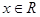 .
.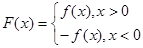
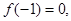 且函数
且函数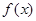 的值域为
的值域为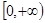 ,求
,求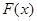 的表达式;
的表达式;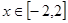 时,
时,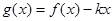 是单调函数,求实数
是单调函数,求实数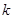 的取值范围;
的取值范围;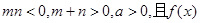 为偶函数,判断
为偶函数,判断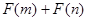 能否大于零?
能否大于零?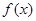 的定义域为
的定义域为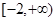 ,部分对应值如下表.
,部分对应值如下表.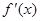 为
为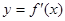 的图像如图
的图像如图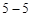 所示:若两正数
所示:若两正数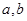 满足
满足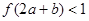 ,则
,则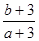 的取值范围是( )
的取值范围是( )





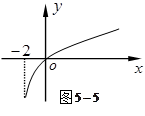
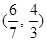 B.
B.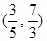 C.
C.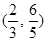 D.
D.