题目内容
(本题满分13分)
已知数列 的前
的前 项和为
项和为 ,满足
,满足 .
.
(Ⅰ)证明:数列 为等比数列,并
为等比数列,并 求出
求出 ;
;
(Ⅱ)设 ,求
,求 的最大项.
的最大项.
已知数列
 的前
的前 项和为
项和为 ,满足
,满足 .
.(Ⅰ)证明:数列
 为等比数列,并
为等比数列,并 求出
求出 ;
;(Ⅱ)设
 ,求
,求 的最大项.
的最大项.(Ⅰ)证明:由
 ………………1分
………………1分由
 ,两式相减得
,两式相减得
 ………………3分
………………3分 ………………5分
………………5分
 是首项为
是首项为 ,公比为
,公比为 的等比数列 …………6分
的等比数列 …………6分 . ………………7分
. ………………7分(Ⅱ)解:由(Ⅰ)知
 ……………8分
……………8分由
 ………………11分
………………11分由
 得
得 ,所以
,所以
故
 的最大项为
的最大项为 . ………………13分
. ………………13分略

练习册系列答案
 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目
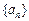 满足条件
满足条件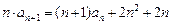 ,
,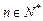 ,
,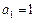 ,设
,设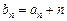

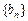 的通项公式;
的通项公式;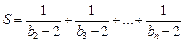 。(14分)
。(14分)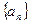 的各项都为正数,其前
的各项都为正数,其前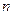 项和为
项和为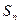 ,已知对任意
,已知对任意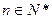 ,
,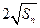 是
是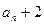 和
和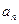 的等比中项.
的等比中项.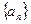 的通项公式;
的通项公式;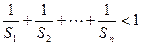 ;
;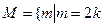 ,
,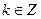 ,且
,且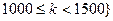 ,若存在
,若存在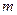 ∈
∈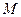 ,使对满足
,使对满足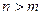 的一切正整数
的一切正整数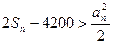 恒成立,求这样的正整数
恒成立,求这样的正整数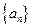 满足关系式:
满足关系式: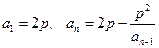 (p是常数).
(p是常数).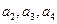 ;
;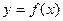 的图象经过坐标原点,与
的图象经过坐标原点,与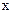 轴的另一个交点为
轴的另一个交点为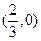 ,且
,且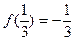 ,数列
,数列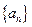 的前
的前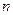 项的和为
项的和为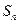 ,点
,点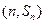 在函数
在函数 ,求数列
,求数列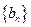 的前
的前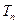 .
. 是首项为
是首项为 ,公比
,公比 的等比数列,设
的等比数列,设 ,数列
,数列 满足
满足 .
. 的通项公式;
的通项公式; 对一切正整数
对一切正整数 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.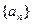 中,
中,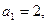 公积为5,当n为奇数时,这个数列的前
公积为5,当n为奇数时,这个数列的前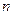 项和
项和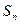 =_________。
=_________。 为等差数列,且
为等差数列,且 ,
, 。
。 的
的 最大值是 。
最大值是 。