题目内容
已知 是关于
是关于 的方程
的方程
 的根,
的根,
证明:(Ⅰ) ;(Ⅱ)
;(Ⅱ) .
.
(Ⅰ)证明见解析;(Ⅱ)证明见解析.
解析试题分析:(Ⅰ)构造函数 ,通过导函数可知函数在
,通过导函数可知函数在 上是增函数,而
上是增函数,而 ,
,
 ,故
,故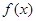 在
在 上有唯一实根,即
上有唯一实根,即 ,然后利用函数的单调性,用反证法证明
,然后利用函数的单调性,用反证法证明 ;(Ⅱ)先证
;(Ⅱ)先证
 ,再由
,再由 ,
, 可得
可得 .注意放缩法的技巧.
.注意放缩法的技巧.
试题解析:(Ⅰ)设 ,则
,则
显然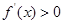 ,
, 在
在 上是增函数
上是增函数


 在
在 上有唯一实根,即
上有唯一实根,即 4分
4分
假设 ,
,
则



 ,矛盾,故
,矛盾,故 8分
8分
(Ⅱ)

 (
( )
) ,
,
 13分
13分
方法二:
由(Ⅰ)

 =
=

考点:1.函数的零点;2.函数的单调性的应用;3.放缩法证明不等式

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目


 的解集;
的解集; 的不等式
的不等式 在
在 上无解,求实数
上无解,求实数 的取值范围
的取值范围 ≤
≤ +
+ +xy;
+xy; ,
, 的解集为
的解集为 ,求实数
,求实数 的值;
的值; 对一切实数
对一切实数 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围. .
.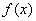 最大值?
最大值? 使
使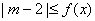 成立,求实数
成立,求实数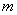 的取值范围。
的取值范围。 -1,证明:
-1,证明: (x-1);
(x-1); .
.