题目内容
18.已知f(x)=(x2-2x)ex(其中e是自然对数的底数),f'(x)为f(x)的导函数,则f'(0)的值为-2.分析 根据函数导数公式求出函数的导数进行求解即可.
解答 解:函数的导数为f′(x)=(2x-2)ex+(x2-2x)ex=(x2-2)ex,
则f'(0)═(02-2)e0=-2,
故答案为:-2.
点评 本题主要考查函数的导数的计算,根据导数的公式求出函数的导数是解决本题的关键.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
8.设全集U={1,2,3,4,5,6},A={1,2},B={2,3,4},则A∩(∁UB)=( )
| A. | {1,2,5,6} | B. | {1,2,3,4} | C. | {2} | D. | {1} |
9.已知集合A={1,4},B={y|y=log2x,x∈A},则A∪B=( )
| A. | {1,4} | B. | {0,1,4} | C. | {0,2} | D. | {0,1,2,4} |
13.已知双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1({a>0,b>0})$的焦点到渐近线的距离为2,且双曲线的一条渐近线与直线x-2y+3=0平行,则双曲线的方程为( )
| A. | $\frac{x^2}{16}-\frac{y^2}{4}=1$ | B. | $\frac{x^2}{8}-\frac{y^2}{4}=1$ | C. | $\frac{x^2}{4}-{y^2}=1$ | D. | ${x^2}-\frac{y^2}{4}=1$ |
3.某石材加工厂可以把甲、乙两种类型的大理石板加工成A,B,C三种规格的小石板,每种类型的大理石板可以同时加工成三种规格小石板的块数如表所示:
某客户至少需要订购A,B两种规格的石板分别为20块和22块,至多需要C规格的石板100块,分别用x,y表示甲、乙两种类型的石板数.
(1)用x,y列出满足客户要求的数学关系式,并画出相应的平面区域;
(2)加工厂为满足客户的需求,需要加工甲、乙两种类型的石板各多少块,才能使所用石板总数最少?
| 板材类型 | A | B | C |
| 甲型石板(块) | 1 | 2 | 4 |
| 乙型石板(块) | 2 | 1 | 5 |
(1)用x,y列出满足客户要求的数学关系式,并画出相应的平面区域;
(2)加工厂为满足客户的需求,需要加工甲、乙两种类型的石板各多少块,才能使所用石板总数最少?
7.已知O为坐标原点,F是双曲线$Γ:\frac{x^2}{a^2}-\frac{y^2}{b^2}=1({a>0,b>0})$的左焦点,A,B分别为Γ的左、右顶点,P为Γ上一点,且PF⊥x轴,过点A的直线l与线段PF交于点M,与y轴交于点E,直线 BM与y轴交于点N,若|OE|=2|ON|,则 Γ的离心率为( )
| A. | 3 | B. | 2 | C. | $\frac{3}{2}$ | D. | $\frac{4}{3}$ |
8.若直线y=x+b与曲线(x-2)2+(y-3)2=4(0≤x≤4,1≤y≤3)有公共点,则实数b的取值范围是( )
| A. | [1-2$\sqrt{2}$,3] | B. | [1-$\sqrt{2}$,3] | C. | [-1,1+2$\sqrt{2}$] | D. | [1-2$\sqrt{2}$,1+2$\sqrt{2}$] |
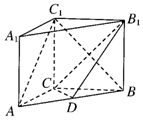 如图所示,在直三棱柱ABC-A1B1C1中,AC=3,BC=4,AB=5,AA1=4,点D是AB的中点.
如图所示,在直三棱柱ABC-A1B1C1中,AC=3,BC=4,AB=5,AA1=4,点D是AB的中点.