题目内容
已知椭圆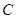 :
: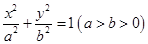 的离心率为
的离心率为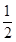 ,
,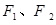 分别为椭圆
分别为椭圆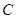 的左、右焦点,若椭圆
的左、右焦点,若椭圆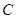 的焦距为2.
的焦距为2.
⑴求椭圆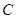 的方程;
的方程;
⑵设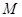 为椭圆上任意一点,以
为椭圆上任意一点,以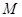 为圆心,
为圆心,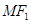 为半径作圆
为半径作圆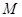 ,当圆
,当圆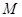 与椭圆的右准线
与椭圆的右准线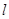 有公共点时,求△
有公共点时,求△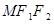 面积的最大值.
面积的最大值.
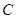 :
: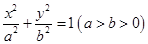 的离心率为
的离心率为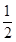 ,
,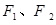 分别为椭圆
分别为椭圆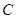 的左、右焦点,若椭圆
的左、右焦点,若椭圆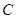 的焦距为2.
的焦距为2.⑴求椭圆
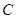 的方程;
的方程;⑵设
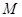 为椭圆上任意一点,以
为椭圆上任意一点,以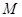 为圆心,
为圆心,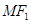 为半径作圆
为半径作圆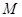 ,当圆
,当圆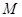 与椭圆的右准线
与椭圆的右准线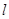 有公共点时,求△
有公共点时,求△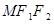 面积的最大值.
面积的最大值.⑴ . ⑵
. ⑵ 。
。
 . ⑵
. ⑵ 。
。试题分析:⑴因为
 ,且
,且 ,所以
,所以 . 2分
. 2分所以
 . 4分
. 4分所以椭圆
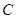 的方程为
的方程为 . 6分
. 6分⑵设点
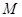 的坐标为
的坐标为 ,则
,则 .
.因为
 ,
, ,所以直线
,所以直线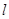 的方程为
的方程为 . 8分
. 8分由于圆
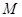 与
与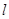 有公共点,所以
有公共点,所以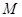 到
到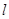 的距离
的距离 小于或等于圆的半径
小于或等于圆的半径 .
.因为
 ,所以
,所以 , 10分
, 10分即
 .
.又因为
 ,所以
,所以 . 12分
. 12分解得
 ,又
,又 ,∴
,∴ . 14分
. 14分当
 时,
时, ,所以
,所以 16分
16分点评:中档题,求椭圆的标准方程,主要运用了椭圆的几何性质,a,b,c,e的关系。曲线关系问题,往往通过联立方程组,得到一元二次方程,运用韦达定理,简化解题过程。利用函数观点,建立三角形面积的表达式,确定其最值。

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
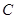 的对称中心为坐标原点,上焦点为
的对称中心为坐标原点,上焦点为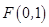 ,离心率
,离心率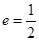 .
.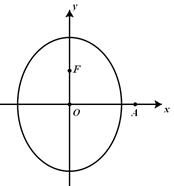
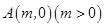 为
为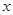 轴上的动点,过点
轴上的动点,过点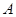 作直线
作直线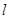 与直线
与直线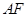 垂直,试探究直线
垂直,试探究直线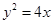 的焦点为F2,点F1与F2关于坐标原点对称,直线m垂直于x轴,垂足为T,与抛物线交于不同的两点P、Q且
的焦点为F2,点F1与F2关于坐标原点对称,直线m垂直于x轴,垂足为T,与抛物线交于不同的两点P、Q且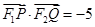 .
.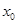 ;
;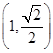 .
.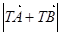 的取值范围.
的取值范围. 
 :
:
 过点
过点 ,上、下焦点分别为
,上、下焦点分别为 、
、 ,
, .直线
.直线 与椭圆交于
与椭圆交于 两点,线段
两点,线段 中点为
中点为 .
. ,若曲线
,若曲线 与区域
与区域 的最小值.
的最小值. ,且它的一个焦点与抛物线
,且它的一个焦点与抛物线 的焦点重合, 则此椭圆方程为
的焦点重合, 则此椭圆方程为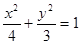



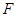 是椭圆
是椭圆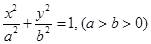 的左焦点,直线
的左焦点,直线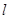 方程为
方程为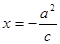 ,直线
,直线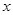 轴交于
轴交于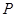 点,
点,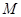 、
、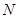 分别为椭圆的左右顶点,已知
分别为椭圆的左右顶点,已知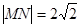 ,且
,且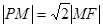 .
.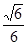 的直线交椭圆于
的直线交椭圆于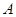 、
、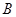 两点,求三角形
两点,求三角形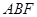 面积.
面积.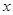 轴上,长轴长等于12,离心率等于
轴上,长轴长等于12,离心率等于 ;椭圆经过点
;椭圆经过点 ;椭圆的一个焦点到长轴两端点的距离分别为10和4.
;椭圆的一个焦点到长轴两端点的距离分别为10和4.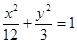 的左焦点为
的左焦点为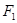 , 点
, 点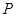 在椭圆上, 如果线段
在椭圆上, 如果线段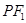 的中点
的中点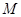 在
在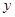 轴的
轴的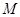 的坐标是 .
的坐标是 .