题目内容
设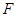 是椭圆
是椭圆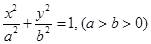 的左焦点,直线
的左焦点,直线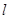 方程为
方程为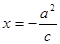 ,直线
,直线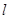 与
与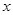 轴交于
轴交于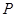 点,
点,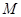 、
、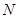 分别为椭圆的左右顶点,已知
分别为椭圆的左右顶点,已知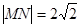 ,且
,且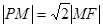 .
.
(Ⅰ)求椭圆的标准方程;
(Ⅱ)过点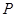 且斜率为
且斜率为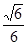 的直线交椭圆于
的直线交椭圆于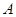 、
、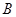 两点,求三角形
两点,求三角形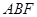 面积.
面积.
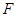 是椭圆
是椭圆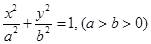 的左焦点,直线
的左焦点,直线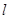 方程为
方程为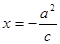 ,直线
,直线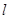 与
与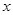 轴交于
轴交于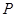 点,
点,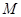 、
、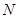 分别为椭圆的左右顶点,已知
分别为椭圆的左右顶点,已知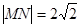 ,且
,且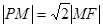 .
.(Ⅰ)求椭圆的标准方程;
(Ⅱ)过点
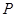 且斜率为
且斜率为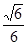 的直线交椭圆于
的直线交椭圆于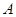 、
、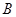 两点,求三角形
两点,求三角形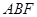 面积.
面积.(Ⅰ) ;(Ⅱ)三角形
;(Ⅱ)三角形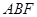 面积为
面积为 .
.
 ;(Ⅱ)三角形
;(Ⅱ)三角形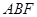 面积为
面积为 .
. 试题分析:(Ⅰ)∵
 ,∴
,∴ ,又∵
,又∵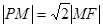 ,
,∴
 ,∴
,∴ ,
, ,
,∴椭圆的标准方程为
 6分
6分(Ⅱ)由题知:
 ,
, ,
, :
: ,
, ,
, ,
,由
 消
消 得:
得: , 9分
, 9分∴
 .
.点
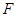 到直线
到直线 的距离:
的距离: , 12分
, 12分∴
 ,即三角形
,即三角形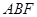 面积为
面积为 . 14分
. 14分点评:中档题,求椭圆的标准方程,主要运用了椭圆的几何性质,注意明确焦点轴和a,b,c的关系。曲线关系问题,往往通过联立方程组,得到一元二次方程,运用韦达定理。本题(2)在应用韦达定理的基础上,应用弦长公式,易于进一步计算三角形面积。

练习册系列答案
 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案
相关题目
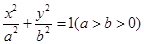 的左、右焦点分别为
的左、右焦点分别为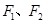 ,离心率为
,离心率为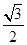 ,点A是椭圆上任一点,
,点A是椭圆上任一点,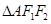 的周长为
的周长为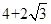 .
.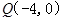 任作一动直线l交椭圆C于
任作一动直线l交椭圆C于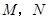 两点,记
两点,记 ,若在线段
,若在线段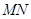 上取一点R,使得
上取一点R,使得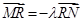 ,则当直线l转动时,点R在某一定直线上运动,求该定直线的方程.
,则当直线l转动时,点R在某一定直线上运动,求该定直线的方程.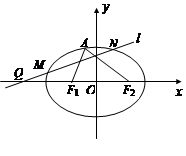
 分别是椭圆:
分别是椭圆: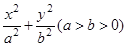 的左、右焦点,过
的左、右焦点,过 倾斜角为
倾斜角为 的直线
的直线 与该椭圆相交于P,
与该椭圆相交于P,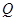 两点,且
两点,且 .
. 满足
满足 ,求该椭圆的方程.
,求该椭圆的方程.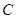 :
: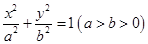 的离心率为
的离心率为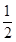 ,
,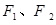 分别为椭圆
分别为椭圆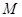 为椭圆上任意一点,以
为椭圆上任意一点,以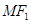 为半径作圆
为半径作圆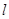 有公共点时,求△
有公共点时,求△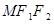 面积的最大值.
面积的最大值. 的左、右焦点分别为
的左、右焦点分别为 、
、 ,若椭圆
,若椭圆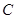 上恰好有6个不同的点
上恰好有6个不同的点 ,使得
,使得 为等腰三角形,则椭圆
为等腰三角形,则椭圆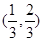



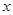 轴上的椭圆的离心率为
轴上的椭圆的离心率为 ,且经过点
,且经过点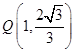 。若分别过椭圆的左右焦点
。若分别过椭圆的左右焦点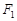 、
、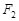 的动直线
的动直线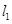 、
、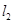 相交于P点,与椭圆分别交于A、B与C、D不同四点,直线OA、OB、OC、OD的斜率
相交于P点,与椭圆分别交于A、B与C、D不同四点,直线OA、OB、OC、OD的斜率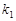 、
、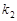 、
、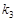 、
、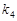 满足
满足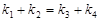 .
.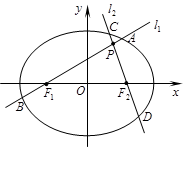
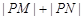 为定值.若存在,求出M、N点坐标;若不存在,说明理由.
为定值.若存在,求出M、N点坐标;若不存在,说明理由. 的一个焦点是
的一个焦点是 ,那么
,那么 .
.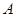 是椭圆
是椭圆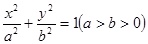 上一点,
上一点,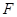 为椭圆的一个焦点,且
为椭圆的一个焦点,且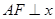 轴,
轴,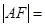 焦距,则椭圆的离心率是( )
焦距,则椭圆的离心率是( ) 
 -1
-1 -1
-1
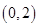 ,且离心率为
,且离心率为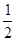 的椭圆的标准方程是________________。
的椭圆的标准方程是________________。