题目内容
已知数列{an}满足an=
+
+
+…+
.
(1)数列{an}是递增数列还是递减数列?为什么?
(2)证明:an≥
对一切正整数恒成立.
| 1 |
| n+1 |
| 1 |
| n+2 |
| 1 |
| n+3 |
| 1 |
| 2n |
(1)数列{an}是递增数列还是递减数列?为什么?
(2)证明:an≥
| 1 |
| 2 |
考点:数列的函数特性,数列的应用
专题:函数的性质及应用
分析:(1)作差判断an+1-an=
+
-
=
-
,符号即可得出单调性,
(2)根据单调性得出an≥a1=
.即可证明.
| 1 |
| 2n+1 |
| 1 |
| 2n+2 |
| 1 |
| n+1 |
| 1 |
| 2n+1 |
| 1 |
| 2(n+1) |
(2)根据单调性得出an≥a1=
| 1 |
| 2 |
解答:
解:(1)∵an=
+
+
+…+
,
∴an+1=
+
+
+…+
=
+
+
+…+
+
+
,
∴an+1-an=
+
-
=
-
,
又n∈N+,∴2n+1<2(n+1),∴an+1-an>0,
∴数列{an}是递增数列.
(2)由(1)知数列{an}为递增数列,
所以数列{an}的最小项是a1=
,
所以即an≥
对一切正整数恒成立.
| 1 |
| n+1 |
| 1 |
| n+2 |
| 1 |
| n+3 |
| 1 |
| 2n |
∴an+1=
| 1 |
| (n+1)+1 |
| 1 |
| (n+1)+2 |
| 1 |
| (n+1)+3 |
| 1 |
| 2(n+1) |
=
| 1 |
| n+2 |
| 1 |
| n+3 |
| 1 |
| n+4 |
| 1 |
| 2n |
| 1 |
| 2n+1 |
| 1 |
| 2n+2 |
∴an+1-an=
| 1 |
| 2n+1 |
| 1 |
| 2n+2 |
| 1 |
| n+1 |
| 1 |
| 2n+1 |
| 1 |
| 2(n+1) |
又n∈N+,∴2n+1<2(n+1),∴an+1-an>0,
∴数列{an}是递增数列.
(2)由(1)知数列{an}为递增数列,
所以数列{an}的最小项是a1=
| 1 |
| 2 |
所以即an≥
| 1 |
| 2 |
点评:本题考查了数列的性质,运用函数求解问题,难度不大,属于中档题,关键是确定解题方法即可.

练习册系列答案
 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案
相关题目
执行如图所示的程序框图,若f(x)=3x2-1,取?=
,则输出的值为( )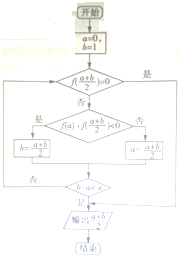
| 1 |
| 10 |

A、
| ||
B、
| ||
C、
| ||
D、
|
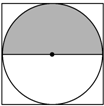 在如图所示的正方形中随机掷一粒豆子,豆子落在正方形内切圆的上半圆(圆中阴影部分)中的概率是
在如图所示的正方形中随机掷一粒豆子,豆子落在正方形内切圆的上半圆(圆中阴影部分)中的概率是